盆地尺度驻波运动

层状分层中的界面波

水平模式当稳定风停止，地表应力条件放松时，重力恢复力与的冠军D界面(水面或温跃层)变得不平衡。体现在倾斜中的可用势能在重力作用下被释放，并在界面以正弦驻波或振动的形式振荡时转换为动能假潮．在盆地端壁和盆地内部的节点(图2和图5)发现了逆波。由于线性波动方程d^n dt2”在空间和时间上很好地描述了波场的演变，因此，逆波通常被称为线性波。

式中^(x,t)为界面位移，co为线性浅水相速度(波峰/波谷传播的速度)。这个方程同样适用于在自由表面或温跃层上传播的界面波，分别适用于表面和内部seiches的适当形式co = y^gff或co = \Jg' h1h2/H。由于相对于自由表面(g’^ g)的重力作用在温跃层上减小，表面波以大约50倍的速度传播内波．

与seiches相关的常见驻波形式是对称的进步的浪潮振幅和波长相同，但符号相反，从盆地两端的上升流和下降流体中传播(图2)。这些波通常用余弦函数表示(图5)，在盆地壁上有中心节点和反结点。对cosc求和

波腹

X / 2节点

波腹

波腹

X / 2节点

波腹

波腹

波腹

波腹

波腹

波腹

波腹

波腹

波腹

波腹

波腹

波腹

波腹

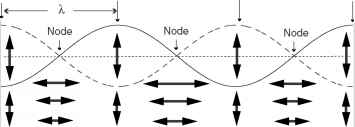
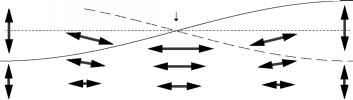
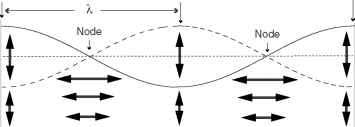
图5原理图显示了前三种水平界面地震模式:水平模式一(n = 1)、模式二(n = 2)和模式三(n = 3)。箭头表示水粒子速度的方向。实线和虚线表示半周期间隔的界面位移。斜压情况的上层速度没有显示出来，可以从对称性推断出来。

图5前三种水平界面地震模式示意图:水平模式一(n = 1)、模式二(n = 2)和模式三(n = 3)。箭头表示水粒子速度方向。实线和虚线表示半周期间隔的界面位移。斜压情况的上层速度没有显示出来，可以从对称性推断出来。

(图5(a))，给出了水平模态1 (H1)驻波模式的方程。

Y (x, t) = a cos (kx + at) + a cos (kx - at) = 2a cos kx cos at

分量波振幅a = dy/2或dys/2取决于所考虑的界面，角频率a = cok，其中k = 2n/X是波数，l是波长，T = 2p/a是波周期。对于封闭盆地，有一半波长的H1地震在湖中，则l = 2L，周期为

tnnco，其中对于H1地震n = 1是水平方向上节点或半波长的数量。

与H1地震有关的层均水平速度在盆地中心最大，由

这些速度在垂直边界处为零，那里的运动是纯垂直的(图5)。与地表地震类似，湖中部深度平均速度为

振荡地震电流具有低周期、准稳态特征。来自各种各样的观察湖泊和水库显示表面和内部地震

04:45

05:27 06:10 07:35

04:45

21:40 00:29 03:19

21:40 00:29 03:19

05:27 06:10 07:35

09:00

纵向当前的速度ulong (cm / s)

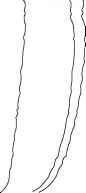
图6 a小湖显示了与地震流有关的振荡性质和防滑边界。观测时间超过地震周期的一半。这些剖面是偏移的，并且都是用给定的速度标度绘制的。(2002)层状盆地低速振荡底边界层湍流动力学研究。环境流体力学2:291-313。

水流的典型范围为0.02-0.20 ms-1，在风暴期间最大为0.2ms-1，在流动受到摩擦阻碍的防滑沉积物边界处趋于零(图6)。

在湖泊中还观测到较高的水平模态扰动(n > 1)。这些由线性波动方程的一个更一般的解来描述，其中初始条件是均匀倾斜的界面，由所有高级水平模式的叠加组成。通解是n = 1v /

水平模态1 (H1)地震时n = 1，水平模态2 (H2)地震时n = 2，水平模态3 (H3)地震时n = 3(图5)。可能存在无限个模态，每个模态的振幅和能量随着模态数的增加而减小。基本解仅由奇数模态组成(即，当n为偶数时-q(x, t) = 0)，正如直观预期的那样，因为只有奇数模态在盆地中部位置有一个节点，在那里有与初始均匀初始倾斜相关的零位移(图2和图3)。通过计算与每种模态相关的APE，可以表明98%以上的波能是但模式间的能量分布受共振强迫和盆地形状的影响较大。

表1给出了各种水平模式下地表和内部地震周期的例子。当波浪随时间周期性振荡时，能量会在势能形式和动能形式之间传递(图2)。在t = 0， (1/2)71 T1， (3/2)T1等时，波浪能量纯粹是势能形式，而在t = (1/4)T1， (3/4)T1， (5/4)T1等时，能量纯粹是动能，在湖盆内产生水平电流(图6)。对于非耗散系统，模态能量分布代表动能和势能的总和，与时间无关。耗散过程会导致波幅的减小，但不会导致周期随时间的减小(表1);除非有足够的混合thermo-cline对于地表地震，振幅随每个连续周期的衰减范围从3%(日内瓦湖)到32%(伊利湖)不等。

垂直模态当垂直密度结构近似为三层或三层以上流体层时(图1c,d)，除垂直模态1、水平模态1 (V1H1)模态外(图2b)，还支持较高的垂直模态模态;例如V2H1等(图2c)。对于三层系统，co等于

where g = (1 - pjp2)hlh2 + (1 - Pi /p3)hlh3 + (1 - p2 M)h2h3 and a = h1 h2h3 (1 - Pl = p2) (1 - p2 /p3):

将波周期Tn = 2L/nco代入方程，得到垂直模态的周期- 2

表1观测到的各种湖泊地表和内部地震周期及相关振幅衰减

湖泊和位置T (h) T2 (h) T3 (h) T4 (h) T5 (h)振幅随每个连续周期的分数下降

坦噶尼喀(非洲)1欧恩湖(苏格兰)1山中(日本)1,2加尔达(意大利)1'2

日内瓦(瑞士-法国)1,2 Vattern(瑞典)1,2贝加尔湖(俄罗斯)1密歇根(加拿大-美国)1伊利(加拿大-美国)1'2内塞奇巴尔德格(瑞士)3卢加诺(瑞士-意大利)4温德米尔(英国)3苏黎世(瑞士)5尼斯湖(苏格兰)3日内瓦(瑞士-法国)3

0.075	0.038	0.028
0.24	0.14	0．10
0.26	0.18	0.09
0.72	0.48	0.37
1．2	0.59
3．0	1．6	1.3
4.6
9.1	5.2	3．7
14.3	9.0	5.9
9.3	4.6	3．1
24	12	8．0
24	13	9
45	24	17
57	27	18
74	46	0.099 4.2 - 0.322 14日11 22日18 1Wilson W (1972) Seiches。在ChowVT (ed)。水文科学进展8:1-94。 2Wüest AJ和Farmer DM (2003) Seiches。在McGraw-Hill科学和技术百科全书，第9版。纽约州:McGraw-Hill。 3Lemmin U和Mortimer CH(1986)在真实湖泊中确定地表地震特征的Defant程序的内部地震扩展试验。湖沼与海洋31:12 7-12。 4Hütter K, Salvade G，和Schwab DJ(1983)卢加诺湖北部盆地的内波动力学。地球物理和天体物理流体动力学27:299-336。 5Horn W, Mortimer CH和Schwab DJ (1986) Wind-indüced Lake内部seiches Zürich观测和建模。湖沼科学31:1232-1254。 波，其中水平模态结构由n定义。 当分层层的上下界面倾斜不对称时(日、季节界面倾斜)，可产生垂直两模态斜温层或者是金属胞元的上下边界)。实验室和有限的现场数据表明，在上升流条件下，这种不对称是由分别发生在顺风岸和逆风岸的金属微粒的压缩和膨胀引起的(例如，图3(d))。竖直模态2响应的强度被假设依赖于威德伯恩湖数和湖数的相对值。小W和大LN(上部界面的强烈倾斜，表层基底的大剪切和相对不受扰动的下部界面)出现V2响应;而小Wand大LN时则发生V1响应(两个界面的倾斜度相当，在低细微离子中有很强的速度)。 在一些湖泊中观测到较高垂直模式的盆地尺度内波，通常是在突然的风脉冲激发了初始的V1H1响应之后，然后演变为V2地震(例如伍德湖、上神秘湖、康斯坦斯湖)。与风强迫的共振(如Alpnach湖)，倾斜的盆地地形和分层层之间不均匀的密度差异可以导致这种更高垂直模式的优先激发。 连续分层中的内部模式 两层假设湖泊分层不适合大多数人吗浅水湖泊(H < ~ 15 m;例如，Frains湖)和非常深的湖泊(如贝加尔湖)或分层具有显著化学(盐)成分的湖泊(如Mono湖)。使用连续分层对这些系统进行更好的建模，其中LN捕获了由风设置引起的等斜线的倾斜。在风应力松弛时，连续的分层将支持垂直盆地尺度模式谱。与每个模态相关的频率由 这取决于盆地的几何形状，可用于计算波周期T = 2p/o。每个垂向模m的结构用波函数Cm描述，Cm是由常数N的线性长波方程得到的 Cm(z) = sinjp z， M = 1,2,3，是某一深度内地层在波浪作用下的垂直位移量。例如，V1波在中深度处的内位移最大，而V2波在1/4H处的位移为正，在3/4H处的位移为负(图7a);显示地层特有的开口。 波函数不包含实际波幅，因此通常归一化- 1 < Cm < 1。Cm的实用在于，它可以从任意N(z)剖面的泰勒-戈尔茨坦方程进行数值计算，从而确定由特定水柱分层所支持的波模式。盆地尺度垂直模态结构可以是单模态结构，也可以是多模态结构，当振幅已知时，可以计算-q(z, t)«Cm(z)a(t)。垂直模态结构可以在整个盆地的空间和时间上投影，方法是假设一个波剖面■q(x, z, t)«Cm(z)v(x, t);这通常是seiches的余弦函数，或孤立波的sech2函数(稍后描述)。 由波动引起的水平速度剖面随波函数codCm/dz的梯度成比例(图7(b))。速度场的解析表达式可以在分层流动文本中找到。图7中的连续速度剖面与图2中所示的深度平均水流一致。在这两个模型中，尽管技术上不正确(图6)，但都假定了自由滑移的底部边界。因此，这些模型的速度不能代表底部边界附近的流动。

继续阅读:湖泊盆地尺度内波的退化

这篇文章有用吗?

＋1 0