湖泊盆地尺度内波的退化
了解导致波浪退化的因素一直是湖沼学家的主要目标。这是因为内波最终它们的能量(简并)在湍流区耗散(毫米尺度下流体的粘性摩擦加热)和双旋流混合(垂直于等旋流或恒密度表面的流体的混合)。反过来,混合驱动生物地球化学通量。湍流直接产生于地震诱发的电流,通过湖泊内部和TBBL中的流体紧张,以及与地震产生不耦合的过程,如表面波破碎和流入,这些过程也会破坏地震运动。作为一般规则,对于深湖,的时期内部假潮每40米水柱衰变约1天
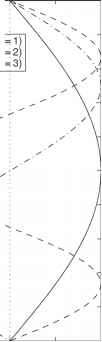
波函数,y
1 |
', j |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1✓ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
/ ' |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
" / / |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
————” |
y |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
/ / |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
/ |
/ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
- / |
/ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 / |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\ / ' |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
_ \ - |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
/ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
/ ^ _ 1 ^ ^ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\ / \ / |
年代 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
- - - - - - \ |
X” |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\ j |
\ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\ / |
1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
_ ' j |
/ - |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
/ \ |
/ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
/ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
N |
' |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
- < * |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
——“ |
\ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1, |
图7 (a)恒N层支持的垂直模态一(m = 1)、二(m = 2)和三(m = 3)的波函数剖面。(b)波函数的特征速度剖面codC/dz见面板(a)。 深度。对于非常深的湖泊,例如H = 1637m的贝加尔湖,这相当于一个多月的衰减期。 现场观测表明,盆地尺度内波的退化主要是由于TBBL内部而非内部的湍流产生的;在底栖边界层中所观测到的耗散和混合现象,是内部的十倍以上(见底栖边界层(在河流中,湖泊和水库))。退化可能通过以下四种机制发生:(1)TBBL中地震流的粘性阻尼,(2)内部剪切不稳定的形成,(3)非线性内部波的产生,在斜坡地形上破碎;(4)内部水力跳跃的形成。通过计算每种机制发生的时间尺度,已经划定了特定机制将占主导地位的区域(图8)。区域是根据逆韦德伯恩数W= / h1和的深度来定义的季节性温跃层(h1 / H)。尽管该状态图严格适用于与分析中使用的矩形系统相匹配的狭长湖泊,但它已被证明可以适当地预测来自各种湖泊的现场观测结果(表2)。退化状态描述如下。 深湖/浅温跃层浅水湖泊/深温跃层 图8显示退化机制的分析区图湖面在长条形的湖泊里。由归一化初始强迫尺度= fyi/h1和季节温跃层深度(h1 /H)表征。实验室观测结果也被绘制(*,开尔文-亥姆霍兹(K-H)波浪和孔;破碎的undularbore;一、孤浪;□、陡化;O,阻尼线性波)。Horn DA, Imberger J, and Ivey GN(2001)湖泊大尺度界面重力波的退化。流体力学学报434:181-207。  浅湖/深温跃层 区域1:阻尼线性波 在相对平静的条件下(W^1 < - 0.2),会产生微弱的阻力,这些阻力会受到TBBL粘度的抑制。地震振幅和电流不足以产生孤立波、剪切不稳定性和/或超临界流。该状态对应于图4中的状态A。盆地尺度地震TD与粘性阻尼相关的时间尺度由地震能量与底栖边界层能量耗散率的比值估算: 湖面波动能量 etbbl Lake volume TBBL volume 1至10天(适用于中等大小的湖泊) 湖泊内部的能量耗散被忽视了,因为观察性研究表明,湖泊内部的能量耗散。更复杂的粘性地震衰减模型可以在下面的参考文献中找到。 体制4:开尔文-亥姆霍兹波浪 开尔文-亥姆霍兹不稳定性可以由许多机制形成。在强强迫条件下,当温跃层接近中等深度(> -0.8和> -0.3)时,地震诱发的电流将足够强,以克服分层的稳定作用。剪切不稳定性会在孤立波产生和/或地震被粘性阻尼之前发生。来自其他过程的切变,如地表风应力,可以增加地震诱发电流的切变,并在较弱的强迫条件下诱发不稳定。 剪切不稳定性表现为高频内波,这是贯穿湖泊和海洋的金属元胞体的共同特征。这些波是不稳定性发展的早期阶段,具有正弦波形,频率- 10~2Hz,波长- 10~ 50 m,振幅- 1 ~2 m。根据分层和速度剪切剖面的特殊性,剪切不稳定性可以根据它们的剖面进行分类(例如,开尔文-亥姆霍兹波浪、霍姆波或它们的组合)。不稳定性从流动中的微小随机扰动以指数方式增长,导致局部湍流混合或翻滚的斑块状快速退化(参见小规模湍流和混合:能量通量分层的湖泊).这个过程如图9所示。 在连续分层流动中,稳定行为受泰勒-戈尔茨坦方程的控制,从中可以看出梯度理查德森数
大部分观测值落在2 > ~ 0.3),内震将退化为非线性内波。温德米尔地区的斜压倾斜较弱< ~ 0.3),主要响应为阻尼地震。继Horn DA, Imberger J,和Ivey GN(2001)湖泊大尺度界面重力波退化。流体力学学报434:181-207。来源 1.Thorpe SA, Hall A, and Crofts I(1972)尼斯湖内部涌浪。自然237:96-98。 2.莫蒂默CH和霍恩W(1982)内波动力学及其对苏黎世湖浮游生物的影响。Vierteljahresschr。Naturforsch。全球经济。南京大学学报(自然科学版)27(4):344 - 344。 3.希普斯NS和拉姆斯巴顿AE(1966)风对一个狭窄的双层湖的水的影响。伦敦皇家学会哲学汇刊259:391-430。 4.Farmer DM(1978)长非线性内波的观测在湖中.物理海洋学报8:63-73。 5.Hunkins K和Fliegel M(1973)塞内卡湖中的内波状浪涌:孤子的自然发生。地球物理学报78:539-548。 6.Wiegand RC和Carmack E(1986)深温带湖泊内波的气候学。地球物理学报91:3951-3958。 7.李敏(1987)Baldeggersee内波的结构和动力学。湖沼科学32:43-61。 8.张建民(1998)层状湖泊内波天气。湖沼与海洋43:1780-1795。 大部分观测值落在2 > ~ 0.3),内震将退化为非线性内波。温德米尔地区的斜压倾斜较弱< ~ 0.3),主要响应为阻尼地震。继Horn DA, Imberger J,和Ivey GN(2001)湖泊大尺度界面重力波退化。流体力学学报434:181-207。来源 1.Thorpe SA, Hall A, and Crofts I(1972)尼斯湖内部涌浪。自然237:96-98。 2.莫蒂默CH和霍恩W(1982)内波动力学及其对苏黎世湖浮游生物的影响。Vierteljahresschr。Naturforsch。全球经济。南京大学学报(自然科学版)27(4):344 - 344。 3.希普斯NS和拉姆斯巴顿AE(1966)风对一个狭窄的双层湖的水的影响。伦敦皇家学会哲学汇刊259:391-430。 4.Farmer DM(1978)湖中长非线性内波的观测。物理海洋学报8:63-73。 5.Hunkins K和Fliegel M(1973)塞内卡湖中的内波状浪涌:孤子的自然发生。地球物理学报78:539-548。 6.Wiegand RC和Carmack E(1986)深温带湖泊内波的气候学。地球物理学报91:3951-3958。 7.李敏(1987)Baldeggersee内波的结构和动力学。湖沼科学32:43-61。 8.张建民(1998)层状湖泊内波天气。湖沼与海洋43:1780-1795。 是不稳定性的必要条件,但不是充分条件(Miles-Howard准则)。波浪沿流动中的薄层(-10厘米厚)发生,在这些薄层中Rig较低,并且有明显密度梯度的界面。通过翻滚,界面变得更加弥散,并被厚度为d - 0.3(AU)2/g'的剪切层所取代,其中AU为界面上的速度跳变。由于翻滚,除非AU增加(例如,由于风应力增加)或d减少(例如,由于混合层加深),否则流动变得稳定。在理论上,不稳定的谱是可能的,但最不稳定的模式波的波长为A = 2p/k - 7d。 将Taylor-Goldstein方程应用于现场观测表明,最不稳定模态的频率刚好低于通过金属离子的最大浮力频率。这是因为流体包裹垂直偏离平衡密度位置,就像在不稳定的增长过程中发生的那样,将受到相对于周围环境的突然密度异常所产生的浮力的影响。流体包裹将以频率N的波振荡,直到运动被粘性摩擦阻尼或演变成波涛并崩溃为湍流。流体包裹不会在频率大于N时自然振荡,因此波不会在这些频率上传播;因此N是内波运动的极限高频截止值。 由于斜压流在层间界面上的反转,内部夹层产生了大量的垂直剪切(图2-5)。这种剪切的幅度是周期性的,当界面是水平的(如T1/4)时,其值最大波能是在动力学形式中。可以在分离离散层的接口上应用大量Ri 预测不稳定性的形成。如果本底流是时变的,要么Ri = 1/4条件的维持时间必须长于不稳定Th - 20(AU)/g’的生长和翻滚周期,要么Ri必须<<1/4。湖泊中的Th值为分钟或更短的数量级。 剪切不稳定可能发生在湖泊的节点位置,在那里垂直切变最大,在强风条件下的表层底部,在温跃层的上下表面  图9 Kelvin-Helmholtz剪切不稳定性的增长和湍流退变示意图,导致分层流体的双喷流混合。该条件在(a)中表示为速度(u)和密度(p)剖面,在(b)中表示为等斜面,其中箭头表示流动方向。在(B -j)中,A和B是流动中的固定点,直线表示等密度曲面(等斜线)。改编自莫蒂默CH(1974)。湖泊水动力学。分层流体中过渡现象和湍流的发展:综述。地球物理学报92:5231-5248。 在河流进水口和水库回撤层附近,以及在有水流经过粗糙地形的地区,由金属膜层垂直二型压缩产生的喷流。 状态3:超临界流 分层流动从超临界(Fr2 + Fr| > 1)过渡到亚临界(F^2 + Fr^ < 1)流动条件时发生内部水力跳变,其中上层和下层弗鲁德数定义为Fr2 = U2 / g'h1和Fr^ = U22 / g'h2。虽然它们在海洋中更常见,是潮汐流过地形特征的结果(例如,奈特湾基岩);湖泊中可能发生内部水力跳跃。 当超临界流(由重力流产生,流入,风事件或温跃层喷流)传播到一个未受干扰的区域。流过地形特征可以导致在障碍物的背风处静止跳跃。局部能量耗散和混合发生在跳跃附近,波从Fr = 1的临界点辐射。 湖泊水力现象的影响和分布还没有很好地了解。 状态2:孤波 在中等强迫作用(0.3 < W-1 < 1.0)的中小型湖泊中,非线性变得显著,线性波动方程不再完全描述波浪演化。除了线性驻波(由对称余弦分量以驻波模式组合而成)外,风诱导的温跃层倾斜还产生了非对称非线性波分量。不对称分量结合成一个渐进的内波模式。下井流体形成一个弥散的亚盆尺度的凹陷内波包(图10),称为非线性内波(NLIWs),而上升流则演化为递进的盆尺度非线性波,称为稀疏波或内浪涌。 弱非线性Korteweg-de-Vries (KdV)方程从数学上描述了由风致温跃层形成的NLIW的产生和单向发展 其中非线性系数a = (3co/ 2)(h1 - h2)/ h1h2,色散系数b = co h1h2/6。最初,内部浪涌在非稳态(Orç/ 01)和非线性arç(0rç/ Ox)项之间的平衡下传播。随着波形变陡和波前接近垂直,非线性变得更加明显(图10c)。这发生在变陡的时间尺度上 波变陡导致色散项brç(03rç/ Ox3)变得重要,最终在t = Ts处平衡非线性变陡,导致高频NLIWs的产生(图10d)。 在许多湖泊中,NLIWs的波浪剖面与KdV方程t) = asech2 ^的特定解相匹配 x ct 这些波被称为孤波。由c = co H - aa和12 = 12 - 3 aa分别给出孤波的最大振幅a、孤波速度c和特征水平长度尺度1 风引起的温跃层凹陷 递进内波 递进内波
图10 NLIW包演化示意图(a)最初的风诱导温跃层下降,(b-c)通过非线性变陡形成渐进式浪涌,(d-e)在t = Ts时形成分散的NLIW包。对于所示的情况,风吹的时间小于T1/4,整个温跃层没有达到稳态倾斜(即没有发生上升流)。这在长(-100公里)狭窄的湖泊(如塞内卡湖、巴比恩湖等)中很常见。 图10 NLIW包演化示意图(a)最初的风诱导温跃层下降,(b-c)通过非线性变陡形成渐进式浪涌,(d-e)在t = Ts时形成分散的NLIW包。对于所示的情况,风吹的时间小于T1/4,整个温跃层没有达到稳态倾斜(即没有发生上升流)。这在长(-100公里)狭窄的湖泊(如塞内卡湖、巴比恩湖等)中很常见。 KdV方程揭示了孤立波的一些有趣特征。在两层体系中,它们总是突出到较厚的层中,因此通常被观察到是温跃层上的凹陷波。如果界面发生在中深度,则a!0;从而防止非线性变陡和随后的孤立波的产生。此外,a对h - h2的依赖关系表明,非线性程度不仅与界面位移的大小有关,而且与分层层的相对高度有关。 从波幅a与波速c之间的关系可以明显地看出波包的色散特性;特定数据包中的波谱将根据振幅排序(图10e),并在传播时随时间分散。孤立波的数量及其振幅的估计,虽然超出了本文的范围,但可以从薛定谔波动方程中得到。 表面孤子 内部孤子 表面孤子 内部孤子  图11内部孤立波在两层分层流体中的通过示意图。虚线是水粒子速度的等高线,箭头表示水流的大小和方向。一个振幅为- (p2 - p1) A的小表面孤立波伴随孤立波并引起撕裂或表面光滑。来自Osborne AR和Burch TL(1980)安达曼海的内部孤子。科学208(4443):451-460。 图11内部孤立波在两层分层流体中的通过示意图。虚线是水粒子速度的等高线,箭头表示水流的大小和方向。一个振幅为- (p2 - p1) A的小表面孤立波伴随孤立波并引起撕裂或表面光滑。来自Osborne AR和Burch TL(1980)安达曼海的内部孤子。科学208(4443):451-460。 实验室实验表明,NLIWs可以包含高达25%的由风引入内波场的能量(APE)。在大型湖泊中,它们的振幅和波长分别可达- 20米和- 50-1000米,传播速度为c - 0.5-0.75 ms-1。通常在海洋中发现的大振幅NLIWs的速度场将在水面上形成一个滑溜(撕裂)(图11),使其能够使用岸基、航空或卫星图像进行定位和跟踪。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
继续阅读:连续分层中的渐进内波射线
这篇文章有用吗?
