Cd牛顿雷诺数
Cd =牛顿的无量纲阻力系数和=颗粒投影面积的方向流动。Cd随雷诺数。用方程(11.24),(11.25)和(11.26)方程(11.23),一个表达式获得粒子的动态行为:
德国焊接学会Cd * * pe * vs2
dt - 2
在最初的瞬态阶段加速度为零和速度是恒定的。这个速度从方程(11.27)可以得到:
vs = ((2 g (p-perV) / (Cd * pe *)) 1/2 (11.28)
如果粒子是球形,直径d, V /等于2/3 * d和方程(6.8)变为:
vs = ((4 g (p - pe) * d) / (3 cd * pe)) 1的2 (11.29)
牛顿的阻力系数Cd,正如前面提到的,雷诺数的函数和粒子的形状。Cd和雷诺数的关系对球体和圆柱体在图11.6中给出。
当雷诺数小于1,Cd和再保险之间的关系可以用Cd = 24 / Re,近似Re =雷诺数定义为:
^ =粘度在哪里
在这种情况下(11.29)符合斯托克斯定律:
vs = _ (p-pe) * d2 (11.30)
18 / y
-
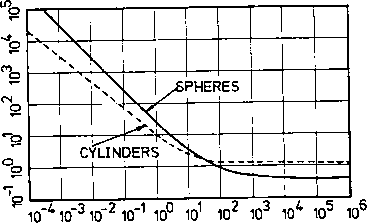
- 图11.6。实验阻力系数与雷诺数的变化。在公平的et al。(1968)。
从图11.6可以看出,Cd大约是常数的湍流雷诺数在1000年和250000年之间的范围。这个地区的速度与:
v8 = 1.82 (((p - pe) * d * g) / pe) 1/2(球体)(11.31)
斯托克斯定律可以修改占对于浮冰通过使用一个“等效半径”和形状系数公式:
2 g R2 (pp - pw) Vs = ___ (11.32)
Vs =沉降速度、长度/时间g =重力加速度,长度/时间^
R =等效半径(基于等效体积的球),页长度=细胞的密度,质量/ length3
pw =水的密度质量/ length3 v =运动粘度Fs =形状系数
形状系数有值< 1.0,占所有因素,减少沉降速度。
大多数氮组件是不幸的是容易溶解在水中,这意味着降水不能作为一种简单的解决问题的办法去除氮、磷相比,广泛从废水利用化学沉淀。然而,除氮利用降水可由以下两个过程:
Mg2“1”+ NH4 + + HPO4 - < = >毫克(NH4) P04 (s) + H + (11.33)
溶解的蛋白质+沉淀剂=不溶性蛋白(11-34)
过程(11.33)看起来乍一看是一个非常有吸引力的解决方案,同时作为磷酸盐和铵沉淀。两个组件之间的化学计量比不过不适合在市政废水沉淀。磷酸的浓度约为10毫克/ 1或0.3更易与我,而通常是铵作为ammonium-N浓度约为30毫克/ 1或2更易/ l。
这意味着必须添加磷酸,以确保适当的沉淀。这使过程更加昂贵,虽然产品magnesiumammonium-phosphate欣赏肥料。过程因此不被用于去除氮的市政废水除飞行员植物实验意大利巴里。可能会吸引更多的利用过程中,N和P之间的化学计量比是更有利的,但比在大多数工业废料水域比市政废水更为不利。
蛋白质的沉淀,使用不同的沉淀剂如ligno-sulfonic酸、铁(III)氯化,氢氧化钙,glucose-tri-sulfate还是pH-adjustment得到了广泛的应用。降水进行等电点的蛋白质,在哪里不稳定是最容易执行。废水常常包含一个广泛的蛋白质,不可能调整pH值对所有蛋白质同时,这样沉淀的蛋白质不会成为100%有效。
继续阅读:设计的植物氮的化合物的沉淀
这篇文章有用吗?
