热量平衡
-
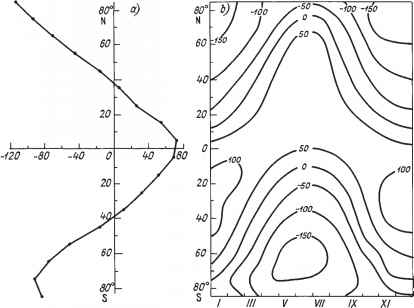
- 图2.2高层大气边界年平均纬向平均净辐射通量(W/m2) (a)及其季节变化(b)。(自Stephens et al, 1981年)
图2.2显示了纬向平均净的时空变异性辐射通量在上层大气边界。请注意三个特征:季节振荡的不对称性,在两个半球的高纬度地区最为明显,局部冬季最大热带与北半球相比,南半球的季节振荡明显增加。第一和第三个特征与出射长波发射的空间分布的具体特征相联系;第二个特征是由于行星反照率的降低导致同化短波太阳辐射的增加。
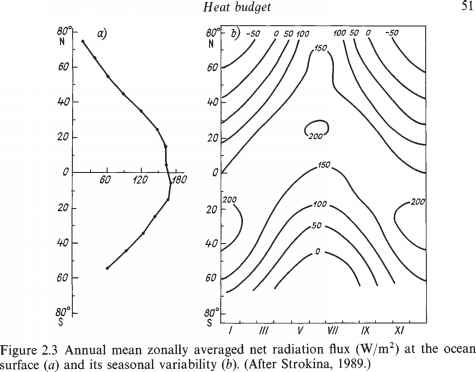
世界海洋表面的净辐射通量也具有同样的特征(图2.3),尽管它们的表现不如上层大气边界的净辐射通量明显。造成这种现象的原因是由于向下长波的存在导致海面有效辐射的减少大气辐射.同样的原因解释了海洋表面净辐射通量与上层大气边界净辐射通量的总和增加。
表示大气中的辐射热流入(大气上层边界和下底层边界的净辐射通量之差
(Qi + Q2),其中Qi和Q2为的流入短波和长波辐射分别。(QÍ + Qf),加上下垫面输入感热,与下垫面感热通量H相等且符号相反热释放=水蒸汽相变引起的LP,以及质量平均感热输送的散度V-cpmAvArA和内能I向势能 ~ cvmATA + V-cpm”^ > = <£+ Qk2 + < & +气- C (< D /) (2.3.1) 这里和上面,TA是空气温度,L是凝结热, cp、CV为定压定容时的空气比热;其余的名称是相同的。 同样,下垫面净辐射通量(Qf + Qf)加上以水蒸气相变为代价的放热量LlEl,减去感热通量Q\ = H和潜热= LE,以及积分感热输移的散度,也必须由海洋或陆地单位柱的热含量变化,即dt来平衡 ^ c0m0f0 + V•c0/Wo = + Qf - Qf - Q?- lxex, (2.3.2) ^ cLmLfL + V cLm'^>L = Q\s + - - <2? 其中c和T为比热比温;M为单位面积圆柱的质量;L,是熔化(升华)的热;下标O和L表示属于海洋和陆地,双上标OS和LS表示属于海洋和陆地表面,符号表示如上所述,对海洋质量或活动陆地层质量求平均。 式(2.3.2)和式(2.3.3)右边出现的项完全描述了下垫面产生的热流。请注意在未被冰覆盖的世界海洋区域内这种通量的时空分布的一些独特特征(L,£,= 0)。从图2.4中可以看出,对于年平均条件,海洋在低纬度从大气中获得热量,在中高纬度失去热量(南半球中纬度的次极大值来自于a 图2.4海洋表面年平均纬向平均产生热通量(W/m2) (a)及其季节变化(b)(继Strokina, 1989年之后)。 图2.4海洋表面年平均纬向平均产生热通量(W/m2) (a)及其季节变化(b)(继Strokina, 1989年之后)。 Iii v vii ix xi Iii v vii ix xi 潜热通量降低)。在北半球,从大气中流入的热量较低热传递海洋进入大气层的高度比南半球高。由此产生的北半球热通量的季节性变化似乎也更大。这一特征可以用两个半球海洋/陆地面积比的差异来解释。 我们用大气潜热LmAqA和海冰L,m的预算方程对(2.3.1)-(2.3.3)系统进行补充(这里,qA是质量平均空气比湿度;M,是指以表面积为单位的海冰质量)。这些方程是这样的 ~LmAqA + V-LmA^A = L(E - P), (2.3.4) - Lxmx + V•Llmlvl = LXEX + L(P - E), (2.3.5) 8t,其中v为海冰漂移速度的水平矢量。 对式(2.3.1)-(2.3.5)在经度上积分,然后求和,得到等式 2na cos q> - ([cvmAfA] + [c0m0f0']f'0 + [cLmLfjf' l at + [LmAqA] +[¿.m,]/,') + - - (MHTk + MHT0) = 2 na因为< p ([0 f ] + [£>?]) - 2 na因为< p [C (< D /)), (2.3.6) mA(cPvA Ta + LvAqA)a cos
O是子午线感潜热大气中的运输, (foCoMoVoTo + fmrtiiVi + f'LcLmLvLTL)a cos q> d 当前的速度,海冰漂移,河流和地下水运动;f'Q、f[和f'L是单位经向范围的海洋、海冰和陆地的分带。 式(2.3.5)将高层大气边界的净辐射通量([Qf] + [gj])(其中Qf为吸收的短波太阳辐射通量,Qf为长波发射到空间的通量)与大气的散度联系起来经向热传输,以及大气-海洋-海冰-陆地系统的能量变化。让我们讨论最后两个组成部分的时空变异性。但首先我们考虑季节变化全球热量预算,由等式表示 ({cvmAfA} + {LmA4A} + {c0m0T0} f0 + {cLmLTL} fL + {AmJ /)不能 继续阅读:ZrWK Mi TOl Wofo 这篇文章有用吗?
