一些模型
我们区分单位经向地带性带的扩展气候系统。相应的热预算方程年平均条件的形式
我(x) + V•MHT (x) = iS0S (x) (x, x),(5.4.1之前)
左边第一项描述,和之前一样,即将离任的长波辐射,第二项描述的分歧经向热传输集成在大气的厚度和海洋;右边这个词描述了短波吸收的太阳辐射气候系统;一个(x) = (1 - (x))是当地的吸收系数;其他符号都是相同的。
我们补充方程(5.4.1之前)表示每个函数的年平均纬向平均表面空气温度T (x)和适当的边界条件在两极。我们假设经向热传输是零在赤道和两极。确定我(x)和(x)我们使用提出的近似Budyko(1969),也就是说,我们假设我(x) = A + BT (x),在T (x, x) = (x) < Ts和(x, x) = cij T (x) > Ts,,因为在前面的部分中,A和B是数值常数,在和aj短波太阳辐射吸收系数在冰雪覆盖和无冰纬度区域;Ts = -10°C是一年一度的平均地表气温之间的边界(x = x)这些纬度区。
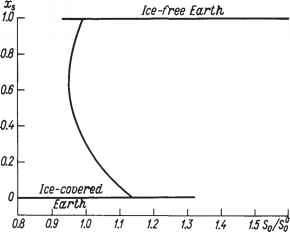
前处理参数化的经向热传输分歧,我们认为,根据北et al。(1981),两种极端情况下,MHT (x) =无穷大和零。在第一种情况下所有纬度上的表面空气温度必须保持相同的,也就是说,一维模型将繁殖情况类似于一个零维模型所描述的。各自的解决方案符合一维模型必须配合,如图5.1所示,唯一的区别是,在温度变化的范围从-15°C到+ 15°C固体曲线在图5.1现在取而代之的是一个扩展的虚线实线代表的解决方案的政权无冰(黑暗)和冰雪覆盖的地球(白色)。破碎的物理解释在相平面曲线(T, S0 /平方)是明显的:为减少太阳常数有降低表面空气温度的等温星球。后者仍然是黑暗的地方表面空气温度达到-10°C,这颗星球后突然变成了白色。新(适合白色政权的星球)表面空气温度为-44°C。
在第二极限情况(零经向热传输)方程(5.4.1之前)减少表单
害怕BT (x) = A + s0 (x) (x) *»)•(5.4.2)
如果一个在x = x (x, x)之间的平均价值在aj7,应用方程(5.4.2)冰雪覆盖和无冰的纬度区域之间的边界,我们获得S0 (x) = 4 (a + BTs) / S (x),一个= (af +}) / 2。
这个关系定义了太阳常数的值S0提供冰南部边界的设置在一个固定的纬度或另一个。计算结果呈现在图5.2演示相当奇怪的情况:如果我们同意现在太阳的进化理论,根据这些假设太阳常数在地球的地质历史的早期阶段是20 - 40%低于其当代价值,然后问,为什么没有被冰覆盖整个地球正如预测的那样,目前,所有可用的一维气候模式?可以提出了几种解释这个悖论,其中缺水创造的冰层覆盖,和被忽视的负面反馈确定的存在,例如,通过改变混浊和气体成分的气氛等。
我们注意到在这个连接,计算得到的结果
-
- 图5.2依赖南方冰边缘位置S0 / S(>一维模型(运输近似),根据北et al。(1981)。
一个隐式的假设的数值常数A和B的普遍性,事实上,必须改变至少在地质时间尺度上,由于大气中吸收物质的含量变化。还需要考虑这样一个事实:一维模型与零经向热传输不能再现真实的气候系统。事实上,从图5.2可以看到,目前极地冰川作用的南部边界的位置(x = 0.95)是由太阳常数满足的超过其当代价值70%。此外,给定值S0 /平方和xs全球表面平均空气温度等于93°C,在x = x温度发生不连续的50°C(见(5.4.2))。很明显,没有考虑到经向热传输是不可能消除观测数据的差异。
两种方法对参数化的经向热传输散度的框架内一维模型是已知的。第一个(所谓的运输近似)提出了Budyko(1969)(参见Budyko, 1980),第二个(扩散近似)提出了Faegre(1972)和北(1975)。我们讨论这些parametri-zations终于为了建立他们的特点和一般特征。
运输近似。年平均条件确定了气候系统的经向热传输的网络辐射通量在上层大气边界。另一方面,它必须是与平均(大气厚度空气温度。但平均气温的垂直变化小于水平变化,所以垂直平均温度与表面空气温度。换句话说,应该有一个经向热传输之间的关系和表面空气温度分布。这些考虑作为近似的基础的经向热传输散度形式
像之前一样,T0是全球平均地表气温;/ ?x 104 W / m2 = 3.75°C是一个经验常数。
替换(5.4.3),7 (x)的定义,(5.4.1之前)的收益率
BT (x) + A + p (T (x)) = iS0S (x) (x, x)。(5.4.4)
从这里开始,使用表达式
一个+ BT0 = iS0H0 (x),
发现集成(5.4.4)/ x从0到1,我们获得的关系确定的年平均纬向平均表面温度大气层。的形式
T (x) = ab ~ 1 +±S0 [S (x) (x, x) + +特色“1)”1。(5.4.6)
还有待发现的南部边界的位置xs极地冰川作用。使用条件T (x) = Ts在x = x,我们获得
Ts (x) = - AB ~ l + 5 s0 [S (x) f (x, x) + !B ~ 1 H0 (xsy] B ~ 1 (l + / JB-1)”1。
在(x, x) =(+, -) / 2 =平均吸收系数。
xs的依赖S0 / S %来自(5.4.7)如图5.2所示。我们注意的弹跳改变南部边界的极地冰川作用后达到纬度50°。下面解释了这个事实:在极地冰川作用的边界(x = x)保持不变冰面长波辐射通量的固定Ts。正因为如此,当S0 /平方减少,南部边界移动到赤道(xs减少),因此,S (x)增加。同时,全球平均地表气温下降发生,这一增加发生在经向热传输散度。但一旦S0 / S %变得足够小的经向热传输的通量散度增加超过短波吸收太阳辐射和极地冰川作用迅速传播到赤道。
相反的事件序列发生与S0 /平方。然而,快速从部分冰川作用的政权过渡到限制政权(无冰地球)也保存在这里。
扩散近似。与被动标量特征识别热含量时的年平均经向热传输将温度梯度成比例,或者,在T (x) - (1 - x2) 1/2 dT (x) / dx的数值因子称为现象学热扩散系数。因此,经向热传输等于j AT1散度
V■MHT (x) = - D {1 - x2) - dx dx因子D代表了产品的热扩散系数l / a2。
我们利用这一近似和重写方程(5.4.1之前)的形式
J J rp
——D (1 - x2) - + + BT = | s0 (x) (x, x)。(5.4.8)
dx dx
让消失的条件的经向热传输是在赤道和北极边界条件,也就是说,dx
第一个条件等价于一个假设的对称表面空气温度场在两个半球。
我们将找到一个方程解(5.4.8)和D = const的形式在勒让德多项式系列P„(x)。首先,我们回忆的勒让德多项式的形式扩散算子
~ (1 _x2 = n (n + l) Pn (x)
dx dx甚至只有那些指数n满足边界条件(5.4.9)。因此,解决(5.4.8),(5.4.9)可以在表单
T (x) = TnPn (x), n = 0, 2, ____We替代这一扩张成(5.4.8),然后乘以P„(x)和集成/ x从0到1。然后,使用正交性条件乔P„(x)点(x) dx = (2 n + l) _1 < 5„m, < 5„米克罗内克符号,我们获得以下为膨胀系数T„关系:
[n (n + 1) D + B ~) Tn + < 5 0 na = \ S0Hn (5.4.10)
„Hn = H (x) = (2 n + 1)害怕j P„(x) S (x) (x, x) dx的多项式函数的参数x列表(x, x) = a0 + a2P2 (x)北(1975)。
具体来说,当n = 0的关系(5.4.10)减少(5.4.5),从那里,对上述数值常数A和B的值和函数H0 (s)、T0 - 14.97°C。n = 2的值函数H„(x) = H2«-0.5。假设,根据北et al。(1981), DB T2 ~ 1 = 0.310 = -28°C (5.4.10)。如果我们限制自己的第一个两项扩张T k T0 + T2P2 {x) -双模近似替代T0和T2的值,然后计算之间的协议,观察经向分布的年度平均地表气温将会很好。当然,事实上,扩散参数化与观测数据基本一致令人印象深刻。但它应该记住,这是一个幸运的选择的结果参数的双模近似,而不是采用的参数化的优点。顺便说一下,经向的扩散参数化热传输范围内提出的双模近似恰逢Budyko (1969)。的确,用T的定义到扩散算子的表达式得到D =常量和n = 2
d / dx
= 6 dt2p2 (x) = 6 d (_T (x)——),从这里,从T发现j的定义?= 6 d。
确定xs我们跟随北(1975)。而不是T (x)我们引入一个新的因变量——即将离任的长波辐射通量/ (x)。然后方程(5.4.8)是重写的形式
~ - d ' (1 x2) + I = {s0 (x) (x, x), (5.4.11)
接下来,我们现在我甚至勒让德多项式级数的形式,使相同的转换表达式的推导了T,也就是说,我们代替扩张(5.4.11),然后获得的方程乘以P„(x)和集成/ x从0到1。因此我们将[n (n + 1)£> ' + 1] /„= (S0/4) Hn (x)。替换这关系到I = InP„(x), n = 0, 2,……收益率,x = x,
“(x) =参加我Hn (Xs !P ^: \ n = 0, 2,…(5.4.12)
从极地冰川作用的南部边界的位置。
的依赖x平方是如图5.3所示。在其建设扩张(5.4.12)与下标n从0到6包容一直保留。可以看出,附近的S0 /平方= 1 x的函数有几个固定的解决方案。特别是S0 ~ 0.98,有五个解决方案达成一致,分别与无冰地球(x = 1),小(0.99 x %)、中级(0.88 x %),和大(0.30 x«)面积极地冰川作用,和冰雪覆盖的地球(xs党卫军0)。这些解决方案的稳定性可以验证同样的零维模型,即通过添加术语dl c (x, t)与热容系数c / dt,左边的方程(5.4.11)和非平稳的线性化方程对小扰动的固定方案。在执行这种转换北et al。(1981)表明,气候制度相应的极地冰川作用的中间区域,以及x * 1.0
无冰地球

无冰地球
继续阅读:Qt X1 ocaQ Qk2 aivTf v vni QQl Qt
这篇文章有用吗?
