V2
分别是总时间导数的算子和拉普拉斯算子。
去寻找大海水的密度采用Eckart形式的线性状态方程:
1.000 027[a + b(p0 + ps)l,其中a, b和p0是定义为a = 1779.5 + 11.250 - 0.074 592 - (3.8 + O.O10)S的参数;B = 0.698;p0 = 5890 - 380 - O.37502 + 3S;密度以g/cm3为单位;温度为摄氏6度,盐度为%o。
在大气子模式中,流体静力不稳定的出现被认为是可能的。它是用对流调整的方法来解决的,即瞬时平衡温度和盐度的剖面,同时考虑到后者的整体守恒。
除对流外,上层海洋的垂直结构由风混合决定。其效应是在Kraus和Turner(1967)提出的局部上层混合层模型框架内描述的。在海洋表面,假设垂直速度等于零,并考虑了大气子模式中确定的风应力和垂直热盐涡旋通量的分量。底部规定了不流动条件和垂直热盐通量消失条件。在海岸线上,假定速度和水平热盐通量的法向分量为零。考虑海冰厚度受局部因素(吸积、融化、升华等)影响而发生变化的可能性,以及厚度对海冰漂移速度的影响,对海冰厚度的演化方程和边界条件体系进行了补充。
在求解海洋子模型方程时,采用了西海岸附近分辨率较好的标准交错网格。在高纬度,网格步长减小,应用空间傅里叶平滑程序。海洋沿垂直方向分为12层,其厚度随着自由表面到海底的距离的增加而不均匀地增加。
在耦合模型框架内对截断球面扇区进行了首次数值实验。从西到东被120°的子午线所限制,从南到北被±81.7°的平行线所限制。大气和海洋的纬向扩展被假定为除高纬度区域外的所有地方都是相等的。所讨论的域的这种结构类似于北美洲和南美洲相邻的大西洋。在大气中,在边界子午线处规定了周期性条件,在边界平行处规定了无流动条件。陆地和海洋表面被认为是平坦的,海洋深度被认为是4公里。为了克服大气和海洋热惯性不同的困难,实现了人工同步,即将各时间步的海洋状态与时间平均的大气状态相结合。这是使用一个相当于指数滤波器的过程来完成的,当t < 0时,加权函数等于X~1 exp(t/X),当t > 0时,加权函数等于0,其中X是时间常数等于一周。
对模式方程积分结果的分析表明,考虑海洋热输运后,低纬度大气变冷,中纬度大气变热。依次,a温度下降赤道和温带之间的差异导致纬向环流减弱,并且由于斜压大气不稳定,导致温带大湍流的动能和Ferrel经向环流的强度下降。海洋中的热平流也有利于亚热带和极地大气压极值的加深以及温带低气压的加深,提供了海洋加热空气到模型大陆东海岸的运输。寒冷的存在赤道上升流影响海洋热带地区降水率的减少和大陆地区降水率的增加。在副热带和高纬度地区,副热带环流的暖水输送增加了海洋向大气的感、潜转移,增加了大陆东部沿海的降水;在北纬地区,这种输送使大陆西海岸出现了类似的影响。总的来说,计算结果采用耦合海洋-大气模型事实证明,这比那些使用海洋被表示为零热容的“沼泽”的模型更现实。
随后,上述数值实验的主要结果被更详细的计算所证实,并应用于大陆和海洋的真实几何。计算是在一个网格上进行的,网格中大气中有9层,海洋中有12层。取空间步长为500km;将1.3个大气年等同于430个海洋年,实现了大气和海洋状态的同步。
让我们详细讨论一下海洋场的计算结果。虽然还没有达到热状态的平衡,但海洋温度分布与观测到的温度分布非常相似。还可以模拟全球盐度分布的主要特征:大西洋的盐度高于太平洋,而太平洋的盐度则发现南部高于北部。此外,该模式正确地再现了海洋中的经向环流,在赤道形成了上升流,在高纬度形成了下降流。事实证明,经向热传输在亚热带温度盐和漂移组分达到最大值当前的速度都朝着一个方向。另一方面,在漂移和温盐分量方向相反的温带地区,经向热输运减少。
与此同时,计算场与观测场之间不可避免地存在差异海洋特征可以提一下。它们主要涉及对高纬度和极纬度地区温度的高估,对盐度的低估,这在北大西洋明显表现出来,以及整个环流强度的减弱。根据Manabe等人(1979)的说法,最后一种情况以及对高纬度地区冷深水形成速率的低估,可以用模式中日照季节变化的缺失来解释。
模型中包含了日照的季节变化和微小变化(海洋中动量、热量和盐度的垂直和水平涡旋扩散系数由深度函数规定;通过将2个大气年等同于1200个海洋年来进行同步),改善了许多气候特点海洋-大气系统,如北极浮冰的分布和北半球大陆积雪的分布。考虑到日照的季节周期,消除了不现实的大厚度海冰(现在约为3米,而不是以前的35米)和雪的持续积累。
海洋和陆地的纬向平均地表气温的时空分布非常令人满意。具体来说,它已经可以模拟一个相移在温带和低纬度地区,海洋表面空气温度的季节性振荡与陆地温度的振幅相比(滞后)和下降,在高纬度地区,最大值越来越早地出现在靠近极点的地方。最后一个特征是由海冰的影响造成的,海冰阻止了海洋和大气之间的热交换,从而促进了海洋气候向大陆气候的转变。raybet雷竞技最新
就气候特征时空分布的模拟精度而言,对于大气中不同高度的平均气温和上层海洋不同深度的水温的平均值(在南北半球),也可以得出类似的结论。从图5.8可以看出,在陆地面积约占半球面积40%的北半球,季节气温振荡的振幅在接近下垫面时增大,这主要是因为反照率的高变异性与大陆积雪的出现和消失有关。这种特征在南半球是找不到的。该图还显示了海洋上层水温季节循环的不对称性:夏季温度与年平均值的最大正偏离比冬季温度与年平均值的最大负偏离高近0.5°C。造成这种现象的原因是冬季对流的存在限制了海面温度的下降季节性温跃层将温暖的上层与寒冷的深海隔离开来。该模型很好地再现了这一特征。
在大气和海洋中热量含量的季节变化和经向热量输送方面也是如此。Manabe et al.(1975)认为,在温带地区,大气经向热量输送在冬初达到最大值,在夏初达到最小值,这主要是由于斜压不稳定强度的适当变化所致。在低纬度地区,经向热输运甚至变为负的,即由北向南。在赤道地区这是由哈得来环流圈将热量从夏季半球输送到冬季半球。
所获得的数据表明,海洋经向热输送与纬向大气环流的强度密切相关:向赤道的热输送是由于西风的作用,而向极地的热输送则是由于南风的作用东风.在冬天西风带的时候
-
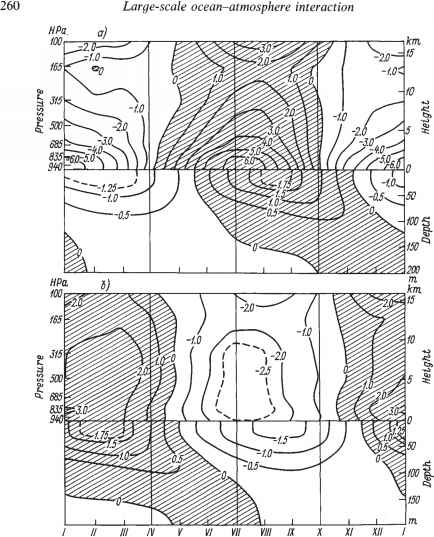
- 图5.8根据Manabe et al.(1979),大气中不同高度的半球平均气温(°C)和海洋中不同深度的水温的季节变化:(a)北半球;(,b)南半球。
东风同时变得更强,向极地的热量输送增加热带在中纬度地区减少。该模型再现的特征与实际数据吻合较好。海洋经向热输送的季节振荡的振幅更不一致(它们被低估了几倍)。但最糟糕的是,这种低估是无法解释的。
北半球中纬度海表温度和南半球高纬度地表空气温度的季节性振荡幅度也被低估了。另一方面,季节性波动的振幅大气的热量高纬度地区的潜热含量以及雪和海冰潜热的季节振荡幅度被高估。Manabe et al.(1979)解释了所列出的差异是云量规定不准确的结果(特别是由于观测数据不可用,假设南半球的云量场与北半球相同),以及地球的质量输运值过低主要洋流.
IOAS模型
该模型的主要区别(见Zilitinkevich et al, 1978)来自于GFDL模型是拒绝人工同步海洋和大气状态,并将海洋细分为与大气自然同步的上层活动层和深海,其状态分别计算。这种方法是为描述相对短期的过程(即季节振荡和年际变化)而设计的,在这种过程中,深海的状态可以被认为是规定的第一近似。
该模式由四个子模式组成:自由大气、大气行星边界、活动海洋层和深海。为了模拟自由大气的气候状态,水热力学方程的使用形式与GFDL模型完全相同;它们只能通过物理过程的参数化方法加以区分。IOAS模式所接受的大气与下垫面之间的小尺度相互作用的参数化是基于相似理论为埃克曼边界层,认为后者淹没在占大气总质量15%的低网格层中。借助方程计算了该边界层的时空变异性,并假设垂直结构是普遍的,即如Ekman边界层的相似理论所预测的那样。
大气与下垫面相互作用特性的计算是在考虑下垫面的影响的阻力、热和水分交换规律的框架内实现的密度分层以及陆地表面粗糙度的变化。下表面温度由热量决定预算方程;在海洋中,这个方程用于确定在海洋-大气界面产生的热通量。在海洋表面有冰覆盖的情况下,其上表面的温度与陆地上的温度相同,也就是说,可以假定冰将海洋与大气完全隔离。对于包括浮冰在内的永久冰盖,引入了表面温度不允许高于0°C的限制。在这种情况下,假定所产生的热流被冰融化所消耗。
IOAS模式使用大气的粗垂直分辨率:后者被分为在1.5、4.5和11千米高度有界面的层。但是,与GFDL模型不同的是,云量不是根据气候数据规定的,而是根据每个时间步的经验公式确定的。的计算方案辐射fluxeS也按照粗垂直分辨率进行了简化。考虑了三级云量和水蒸气吸收的影响。中尺度对流和水汽相变的计算方法与GFDL模型相似,但采用比湿和等效势温对流传递的相似条件,而不是相对湿度随高度的均衡。
由于现有计算机资源的限制,活动海洋层中盐度的影响没有被考虑在内。同时不考虑垂直运动的影响,将活动层中流速的深度平均水平分量分解为借鉴深海子模式的气候分量和风应力决定的漂移分量。它也被认为是热的海洋的结构活动层具有通用性:上层混合层及其下温跃层具有自相似的温度分布。活动层低边界的温度来自于深层子模型,上层混合层的温度和厚度由热和确定狂暴的能量在活动层深度上积分的预算方程。
这些方程由以下算法补充,大致描述了冰盖的影响:如果温度从热量预算海面的方程小于海面水冻结点(- 1.8°C)时,假定出现冰,将活动层与大气完全隔离。据此,假定由此产生的水气界面热流和大气进入海洋的动能流为零,并规定亚冰上层混合层温度为海水冻结温度。在这样做的过程中,上层冰表面的温度是根据海洋表面的热收支方程确定的,假设由此产生的热通量等于零。一旦上层冰层表面的温度高于海水的冰点,人们就相信冰层会消失。
Kagan等人(1974)提出的海洋全球环流二维流体热力学模型被用作深海的子模型。它基于以下假设:海水密度只取决于温度;后者的变化只发生在厚度为2公里的斜压层,在这层以下,温度是固定的,在这层本身,温度表现为竖直坐标的某种标准函数和所需的水平坐标和时间的函数的乘积,这个函数是由整个海洋厚度范围内的热输输方程所决定的。该方程中出现的速度正压分量由积分流函数方程得到;漂移流的垂直平均速度分量由规定的海面风应力由埃克曼方程确定。最后,利用准地转关系估算了垂直平均斜压速度分量。边界条件是这样规定的,以提供实现热和质量守恒定律在世界海洋。
将深海子模式的方程集成到具有5°角分辨率的纬度-经度网格中,从水平均匀(但沿垂直方向分层)海洋的初始状态与其余状态一致,直到建立平衡状态。海洋表面的风应力和由此产生的热流通量是由海洋表面大气压力、空气温度和辐射预算的年平均场,鲍文比固定值为0.5计算得到的。注意,海洋-大气耦合模式只需要提供活动层低边界的当前速度和温度场。
大气子模式方程和活动海洋层方程在Kurihara的球网格上以约1000 km的水平步长进行集成。的年平均经向分布大气温度与海洋上层混合层相比,空气温度的绝热垂直分布、无风以及恒定(在水平面上)的地表大气压值、相对空气湿度并以上部混合层厚度为初始条件。
利用大气和海洋状态的自然同步进行了为期1000天的计算,并考虑了日照的季节周期。大约一年后,大气-活动海洋层系统达到了一个平衡的准周期状态。那时质量平均风速达17 m/s(上层可达40 m/s);大气质量平均温度为244 K;下垫面温度为282 K(南极最低月平均值为234 K,北非最高月平均值为308 K);纬向的平均湿度达1.6 g/kg;云量总分数为0.47;蒸发量和降水量约3.1 mm/d;下垫面净辐射通量达470 W/m2(其中80%用于地球表面长波发射,20%用于蒸发和显热交换)。海洋上空气压比陆地低(994 hPa比1040 hPa),而气温、比湿度、云量、蒸发量和降水则多(分别多5°C、0.9 g/kg、0.4和2.9 mm/d)。
结果表明,该模式能够模拟大气温度、降水、蒸发、云量、热收支组分和海洋表面垂直质量通量的主要时空变化特征,以及上层混合海洋层的特征:温度和厚度。为了证实上述我们特别提到的情况,该模型探测到赤道附近气温季节变化的不对称性,这与两个半球陆地和海洋区域之间的不同关系有关;冬季降水量最大赤道地区在海洋和夏季最大的热带纬度的陆地上;由于下垫面与大气之间的温差增大,冬季海洋和夏季陆地上的蒸发增加;多云:海洋而非陆地上的多云;南北半球海洋表面产生的热通量的季节性振荡之间的六个月相移;最后,海洋温和纬度的质量通量的季节性振荡振幅增加,赤道的最小值全年保持不变。最后一个特征是由于水气温差小和云量的遮挡作用。
利用IOAS模式获得的上层混合层厚度的全球分布表明,从夏季供暖开始,它在温带下降到几十米,在亚热带下降到120-150米。夏季其分布具有较强的空间变异性。在冬季,上层混合层几乎覆盖整个活动海洋层。
CC SBAS模型
该模型(其详细描述可在Marchuk et al, 1984中找到)与上述模型不同的是其更经济的数值算法。它的基础是结合使用两种类型的分裂(对于时间导数算子和平流输运和扩散算子),从而实现质量守恒、角动量守恒、能量守恒(绝热近似)、水分守恒等积分定律。这里需要强调的是,该算法允许我们以比传统差分格式大得多的时间步长来执行积分。
一个CC SBAS模式的大气子模式包含了风速、比湿度和地压的纬向和经向分量的演化方程。为了设计一个绝对稳定的差分格式,前四个方程通过将u, v, T和q转换为变量pll2u, pl/2v, plJ2T和pl/2q而“对称”。水平参数化涡流粘度是在两个条件下进行的。也就是说,描述水平动量扩散的项必须是耗散的,角动量要被保留。满足这些条件的表达式如下:
- kH(j——1- - kHa cos cp -
* * * * * * * * *
式中,a = p/ps, kH为水平涡动粘度系数。事实上,我们用FA乘以u,用F(p乘以v)对整个大气区域进行积分。然后,例如,对于uFx,我们得到uFxa2 cos cp dXd(p =
Cos (pd < pd dip r 3 5 (u
cos3 cp dXdcp < 0,即存在耗散。进一步,我们将Fx乘以cos (p)并对整个大气区域进行积分。作为结果,我们得到
Fxa2 cos2 (p dXd
大气行星边界层的参数化方案简化为挑选出对数层和其上的良好混合层,在此范围内风速、温度和湿度被认为是随高度恒定的。同时,假设行星边界层上边界位置与离下垫面最近的网格面重合,混合层风速矢量与下垫面的风应力夹角保持不变,在一个额外的时间内为30°热带地区陆地上空,海洋上空20°,冰层上空10°。在热带地区,这个角度被假定为零。为了估算海面动量、热量和水分的涡流通量,应用了已知的体积公式,其中阻力和热交换系数与风速和分层有关。
对流调整和大尺度凝结过程的参数化与GFDL模式的参数化相似。采用经验关系式计算云量分数。云的厚度,它们的反照率和吸收能力,以及海洋反照率假定地表和冰层、臭氧和二氧化碳的浓度是固定的。地表反照率在水当量中是积雪厚度的函数。
CC SBAS模式的海洋子模式包含了完整的海洋水热力学方程组,与GFDL模式采用的海洋子模式差别不大。但解法不同。为此,使用了一种分割技术,将扩展的空间操作符分解为许多更简单的空间操作符。与GFDL模型一样,引入了大气和海洋状态的人工同步,其中一个大气年相当于大约100个海洋年。根据100 m厚度的海洋上层混合层的混合特征时间x,选取大气与海洋子模式信息交换的时间采样。对于x = 14天,时间步长等于在大气中40分钟,在海洋中2天,信息交换每6个大气步长和每7个海洋步长执行一次。通过指数滤波器的差分模拟,对传输到海洋子模式的所有大气数据进行时间平滑处理。
所描述的模型在1月的平均条件下进行了测试。计算分两个阶段进行。首先,a2 cos2 cp IdA的平衡态
+ cos
+ cos
对所获得的结果进行分析后发现海洋温度北半球和南半球温带和高纬度地区的增加。这自然会影响大气循环。具体来说,有一个转变热带带降水向南下降约10°,经向温度梯度减小(特别是在南半球),可用势能及其转化为动能的减小(约25%),北半球直接哈德利环流增强,反之则减弱套圈细胞在两个半球,风应力减弱,南半球大陆上空低压中心加深。
考虑到海洋-大气相互作用的影响意味着下列事件的顺序。首先,在太平洋西海岸和印度洋西北部,水温出现负异常,导致强西边界流的出现和上升流的增强。这反过来又导致经向环流的加强,海洋中水平温度梯度的平滑和海洋与大气之间相互作用的减弱。
NCAR的模型
该模式与GFDL模式的区别主要在于大气子模式方程在垂直方向上的有限差分近似;通过子网格尺度的物理过程参数化;并通过大气和海洋状态同步的方法。在NCAR模型中大气分为8层,每层3公里厚。在此基础上,对下垫面动量、热量、水分的辐射通量、云量、涡动通量以及涡动温度的计算方法进行了修正。具体来说,在计算辐射流入时,更精确的吸收函数短波辐射并考虑了不同类型下垫面的吸收特性。明确地描述了日晒量的日变化。低层和中层云的覆盖度由经验关系确定。的基础低端云层位于1.5公里的高度,云的顶部是固定的。中层云被认为是无限薄的。高空云的比例是根据气候数据规定的,它们的基地位于赤道上方10.5公里的高度和两极上方7.5公里的高度;厚度取1.5 km。
计算动量、热量和水分的涡流通量,考虑到阻力和热交换系数对表面大气层的分层和下垫面温度的依赖关系,并考虑到表面的类型。选出了三种类型的下垫面:海洋表面、海冰表面和有植被覆盖和没有植被覆盖的陆地表面。反过来,海冰表面和未被冰覆盖的陆地表面根据它们是否被雪覆盖以及土壤湿度来区分。对于下垫面的每一种类型或子类型,都赋予一定的反照率值,假定它是积雪厚度和太阳天顶角的函数。在植被存在的情况下,考虑了植被覆盖与下垫面的温差、蒸腾与蒸发以及风在植被覆盖中的垂直结构的变化。Washington和Williamson(1977)和Washington et al.(1980)对NCAR模式的大气子模式进行了详细描述。
NCAR模型的海洋子模型与GFDL模型中使用的海洋子模型差别不大。与后者相比,NCAR模型在描述海冰厚度演变的方程中排除了水平输移和摩擦的影响(因此,海冰模型成为一个纯粹的热力学模型),并采用了其他水平和垂直涡动扩散热量和动量的系数值。垂直方向上的离散化是不同的:海洋被分为四层,厚度(从上到下)分别为50、450、1500和2000米。
大气和海洋状态同步的方法可以简化为:海洋子模式方程与5年期间大气参数的固定值(1月、4月、7月和10月)相集成。在对上述四个月的大气子模式方程分别进行积分时,以该时期最后一年获得的下垫面温度和海冰面积作为初始信息。得到的大气参数值假设为第二个五年海洋子模式方程积分时的初始值。同样,找到了每年周期四个月中的每个月对应的大气参数,并继续下去,直到海洋-大气系统的所有环节都建立了准平衡状态。根据Washington et al.(1980)的估计,从计算的角度来看,这种同步方法比已批准的GFDL模型有效十倍。
在第四个五年期间结束时获得的纬向气温、风速的纵向平均纬向分量、海洋表面温度、上层50米层及其下面450米海洋层的洋流速度,以及这些层之间界面处的垂直速度,在质量上与观测结果接近,但在数量上却不接近。例如,1月份的零等温线根据计算结果在北纬38°,根据观测资料在北纬50°。这表明了对北半球冬季气温计算值的低估。其次,根据计算结果,对流层各级夏季气温在40-50°N区域有一个最大值,这没有得到观测数据的证实。我们还注意到高估了南北半球的经向气温梯度赤道区冬季西风进入南半球,夏季西风进入北半球,南半球高纬度地区的计算风速与观测风速(在高度和方向上)存在很大差异。
该模式正确地模拟了海洋表面温度季节变化的主要特征和热赤道的位置。但是墨西哥湾流和黑潮地区的水平温度梯度被低估了,亚热带和中纬度地区的温度值与观测值相比被高估了。第一种情况是由粗糙的(5°)网格分辨率引起的,第二种情况是由于低估了风速及其在海洋和大气之间的热交换和漂移流的热传输中的相关减少。强调指出,对南大洋表面温度的高估导致了南极周围海冰的减少。根据模型作者的说法,这是由于同样的原因和计算的水平涡流热扩散系数值过大。
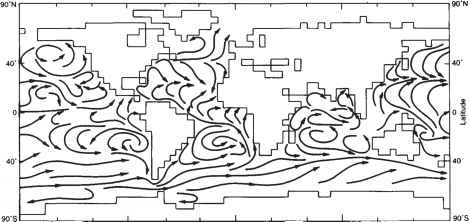
计算场与观测场的定性吻合令人满意。只需说明在第一个网格层(图5.9)中,南极绕极流、墨西哥湾流、黑西奥流、西澳大利亚流、加利福尼亚流和Bengwale流很明显。向西赤道洋流在大西洋和太平洋被发现在第二层网格层,和狭窄太平洋赤道逆流被发现在第一层。一些电流(如Agulhas和拉布拉多犬)根本没有出现
180' 90'w 0 90'e 180'
180' 90'w 0 90'e 180'
180' 90" w 0 90' e 180'
经度
图5.9 1月份世界海洋上层50米层的海流场,根据Washington等人(1980年)。
180' 90" w 0 90' e 180'
经度
图5.9 1月份世界海洋上层50米层的海流场,根据Washington等人(1980年)。
由于网格分辨率较粗。所有电流的速度都是观测到的速度的三分之一。
上面提到的一切都可以应用于垂直运动速度。该模式模拟了强烈的赤道上升流和位于北部15 ~ 20°的下降流区域赤道以南.在这两种情况下,垂直运动的极端速度(根据计算结果和观测数据)都发生在太平洋东部。但是垂直速度的计算值海岸上涌区域比观测到的要小。这个原因是相同的:网格的粗糙空间分辨率。
OS U模型
OSU模型(见Gates et al., 1985, and Han et al., 1985)与GFDL模型的区别主要在于其较粗的水平和垂直分辨率,在许多有待确定的未知数中包含了云量,以及拒绝人工同步海洋和大气状态。
该模型具有以下结构。它由两个大气层和六个海洋层组成。大气的上边界(a - 0)与大气的上边界重合等压面pT = 200 hPa;下界与等压面重合,其中压力p等于表面压力ps;层间界面(a = 1/2)与表面p = (pT + ps)/2重合。每个选定的大气层依次分为两个子层,其界面a = 1/4 (p«369 hPa)和a = 3/4 (p«788 hPa)。
风速、空气温度和比湿度的水平分量是在这些水平面上确定的。等压垂直速度在水平a =1 /2处计算,并假定在水平(7= 0和(7=1)处等于零。海洋层之间的界面位于50、250、750、1550、2750和4350米的深度。所有的层都被中间深度分成两半,在那里,流速、海水温度和盐度的水平分量被计算出来。垂直速度在层与层之间的界面处确定。在海洋表面,它等于零,在海底,它假设等于由运动学关系定义的地形垂直速度。上层50米层被假定为混合良好,中间深度z = 25 m的温度被假定与海面温度一致。水平分辨率(在海洋和大气中相同)预设为纬度4°,经度5°。
如前所述,该模型提供了云量的测定。根据云的形成机制,将云分为四种类型,分别对应于中层a = 1/2的穿透式和积云对流(类型1)、
计算大气的特点它分两个阶段进行:首先(每十分钟)发现由水平和垂直平流决定的变化,然后以内部和外部的热量和动量的来源和汇为代价修正它们的值。非绝热因子每小时讨论一次。对海洋子模型方程进行积分的时间步长为1小时,这样就可以同步海洋和大气之间的热量和动量变化,而不需要任何额外的时间平滑或平均程序。
Han等人(1985)讨论了模拟前16年海洋-大气系统演化的初步结果。这里我们只讨论一些全球性的特征。该模式正确模拟了1月份高层大气边界净辐射通量的最大正值,低估了6月份净辐射通量的最小负值。最后一种情况与低估向外长波有关辐射通量,而后者在南半球冬季和北半球夏季测定云量时又会产生误差。高层大气边界年平均全球净辐射通量为4 ~ 5 W/m2,而不是0,需要处于稳定状态。作者用数值黏度的影响来解释这一特征,并忽略了黏性力将机械能转化为热能。
模型低估了6月和2月下垫面热通量的极值感潜热温带和高纬度海洋冬季的通量,因此不会再现观测到的海表温度变化:在开始积分十年后,计算得出的海表温度季节性波动和观测到的海表温度季节性波动彼此不一致。其原因是南大洋海冰面积的逐渐减少,导致南半球海洋对全球平均海表温度季节性振荡的形成的贡献增加(实际上这些振荡主要由北半球海洋控制)。
我们注意到系统地低估了平均值(大约1.5°C)对流层的温度以及地表空气温度季节性振荡的逐渐增加。对流层平均温度的低估与粗垂直分辨率有关,表面温度季节性振荡的增加与南大洋海冰面积的减少有关。顺便说一下,所发现的缺点(低估了海冰面积,因此高估了南大洋的表面温度)不仅存在于这个模式中,而且也存在于其他海洋-大气耦合环流模式中。但在其他模型中有不同的解释:GFDL模型的作者通过高估吸收的太阳辐射海洋表面的通量和低估漂移流向赤道的热量输送;NCAR模型作者通过高估水平涡旋热扩散系数来解释;OSU模型的作者解释说,在使用水平分辨率较粗的模型时,高估了吸收的太阳辐射通量,也没有充分再现南极上升流。很明显,第一、第二和第三种解释都有一些根据,但尚不清楚这些解释是否充分。
UKMO模型
该模式由大气、海洋和海冰子模式组成。大气子模型是英国气象局气候模型的11级版本,与Corby等人(1977)提出的模型和Slingo和Pearson(1987)提出的模型相比,大气子模型在以下方面更为先进。首先,它包含了由重力波与地球表面地形要素相互作用决定的地形重力波阻力的参数化。第二,假定行星边界大气层包括表面层和上覆混合层及其上覆反转层。假定与反演基相对应的行星边界层高度是可变的。这是借助于在对流不稳定状态下纳入空气夹带的演化方程发现的。在稳定分层的情况下,行星边界层的厚度可以减小到由机械混合决定的最小值。第三,模型描述温度垂直分布在活动土层中。为此目的,土壤温度计算分为四个层次。最后,假设云量是交互的,即由模型生成辐射特性假设云的密度是恒定的,并且等于它们对整个地球的特征值。
海洋子模式由该模式的17级版本表示等密度的扩散和垂直扩散系数与分层的关系。海冰是在热力学模型的框架内描述的,其中预测变量是冰雪的厚度、表面温度和冰的浓度,后者被包括在未知数的数量中,允许存在先导。
模型方程在经纬度2.5°x 3.75°网格上进行积分。海洋和大气子模式之间的信息交换是分开进行的:海洋子模式中边界条件更新所必需的热量、淡水和动量通量,以及大气子模式中边界条件更新所必需的海表温度、海冰面积和浓度,每五天从一个子模式传递给另一个子模式。
Foreman等人(1988)提出的计算数据是对大气-海洋-海冰耦合模式进行四年积分的结果。这样的积分周期不足以达到系统的平衡状态,但对于检测解的变化趋势是可以接受的。特别是,人们发现该模型高估了热带地区的海面温度(有时高估了几度)。造成这一现象的原因之一是对高海温低风速地区感热通量和潜热通量的低估。另一个原因是海表温度与盐度之间存在局部反馈:高估海表温度有助于加剧大气中的对流,后者导致降水增加,地表出现相对淡水层,降水增加静态稳定,垂直混合减弱,最后导致海面温度上升。高估热带海面温度的另一个可能原因是低估了云量,导致高估了吸收的太阳辐射通量。从所提供的数据可以看出,该模式低估了西部边界流的质量输送。例如,墨西哥湾流的最大质量输送结果为35 x 106 m3/s,而从观测来看,它的数量级为100 x 106 m3/s。原因很清楚:网格的粗空间分辨率不允许模拟尺度小于网格尺寸的真实西部边界流。
北半球海洋经向热输运再现不充分,与对西部边界流质量输运的低估密切相关。这解释了在北纬30°北纬以北海面温度计算值被低估的原因。该模型还低估了南大洋海冰面积的季节性变化,根据作者的说法,这是由于忽视了海冰的动态因素造成的。但最糟糕的是,南极海冰的年平均面积往往会随着时间的推移而减少。另一方面,北极的冰面积全年都被高估了,几乎不受季节变化的影响。同样值得注意的是,55°以北的大陆地区夏季地表温度被低估了10-15°C,这与高估了冰盖面积有关。
北半球中纬度地区上空的低空云量被低估了,尤其是在冬季和春季。
这不仅导致了活动地表温度的高估,而且导致了开始的延迟(几乎一个月)雪融化.因此,夏季时间变短,夏季温度比观测到的温度低4-5°C。这种情况还有一个后果:从大陆到北极盆地的平流热传输减少。相应地,北极海冰面积增加,活动地表温度降低。
由于北冰洋吸收的太阳辐射通量夏季值显著降低,上述影响进一步加剧。这不仅是由反馈的存在所决定的反照率和温度而且还低估了入射太阳辐射的两倍多。最后一个特性是由解决云的辐射特性:低端云层的数量在北极变成了现实,但由于他们的辐射特性分配到处都是统一的和遵守全球平均水平值,也就是说,更适合云低和温带的吸收太阳辐射,云太大,和底层表面的太阳辐射通量太小了。所有这一切都因低估大气和海洋极地区的经向热输送而加剧。
MPI模型
起初,这个模型的目的与其说是为了模拟当今气候,不如说是为了演示在解决问题的过程中如何消除一个令人讨厌的特征。raybet雷竞技最新我们指的是所谓的解漂移,即解从一个符合海洋和大气的自主(非交互)模型的稳态到一个与两种介质的交互模型相对应的新稳态的缓慢过渡。这种现象是由独立子模型的不足和它们之间的不匹配引起的,其结果是新的稳态与真实状态相去甚远,尽管两个自治模型在耦合之前已经完全校准并测试了它们与观测数据的一致性。
所提议的程序的本质可以简化为以下内容(Sausen et al, 1988)。如果大气状态的向量被指定为和海洋状态向量*F,如果考虑模型的演化气候系统与真实气候系统演化的误差为:大气为EA,海洋为E0,则描述大气与海洋相互作用演化的方程为:ddf/dt = Ga(
式中GA、G0、F分别为大气和海洋中物质的源、汇以及两者之间的交换;上标“b”表示计算交换所需的函数O和(例如风速、表面大气层的温度和湿度、海面温度等)的边界值。
类似地,描述非耦合大气和海洋演化的方程采用这种形式
< 3 < J > Jdt = GA (4 > U i) + F (< Db、结核病、0 +£,Jdt = Goeru, t) - F (Ob,¥b,我)+ E0 . .
在这里,按照惯例,变量
在(5.8.13)中,我们添加了组件AFA, AF0,并以这样一种方式定义它们,即在交互式和自治模型框架内获得的解应该彼此一致。那么(5.8.13)我们得到以下方程:
d®/ dt = Ga (0 >, t) + F (4 > b,¥b i) +£+阿发,dv / dt =去(^ t) - F (Ob,¥b t) + E0 - AF0 . .
在式(5.8.15)中,我们用和*FU替换®和¥,然后减去式(5.8.14)。作为结果,我们得到
阿发= F (< Db,¥b,我)- F(<魅,¥b,我),AF0 = F«t) - F (< Db,我),
由此可以得出,AFA、AF0是利用经验信息和海洋和大气自主模式信息发现的交换差异,而没有使用经验数据。因此,问题简化为确定对AFA、AF0分量的修正,以及随后对式(5.8.15)的积分。
为了说明这个被称为交换校正过程的过程,我们根据Saussen等人(1988)的观点,检验了我们在1.1节中讨论过的海洋-大气系统的一个简单箱型模型。大气和海洋热收支的演化由以下方程组描述:cA drA/d(= Ra - âaTa + àao(Tq - Ra), c0 dr0/dt = R0 - X0T0 - aA0(Tq - Ta),
其中TA和T0为大气温度和海洋温度;RA和R0为辐射源热源;/A和A0为辐射散热器与各自介质温度之间反馈的参数;Aao为海-气界面的换热系数;cA和cQ是大气和海洋的热容。我们取RA为常数,R0随海洋温度变化为t _ t *1)。
Ro () = {K1 ' + J(°2)_ r°(1)(K2 > - W)在壹空间»< < Tg \ (5.8.18) r {o2)在T0 > P02 \
这样的辐射处方热源考虑到冰雪覆盖反照率与温度之间存在反馈:当T0 < Tq>时,假设海洋表面被冰覆盖;对于T0 > Tq],假定它没有冰。
在使用大气和海洋自主模型的情况下,大气中热收支的演变除其他外,由观测到的海洋温度T{™\的变化控制,而海洋中热收支的演变由观测到的大气温度的变化控制,方程(5.8.17)改写为cA dir/df = Ra - Aa 7T +¿ao(T- 2T), (5.8.19)
c0 dT^/ dT = R0-A0T - aA0(T<0»> - nm))。(5.8.20)
式(5.8.19)有唯一稳态解nu) = (Ra +¿ao TV)/(Xa + kAO), (5.8.21)
而式(5.8.20)可以有一个或三个稳态解,其中两个为稳定解,一个为不稳定解。稳定的稳态解符合式(5.8.18)的上、下两条线,由公式定义
T(ou} = (Rtt + /AO nm))/ AO + /AO), (5.8.22)
其中指数i可以取值1或2,这取决于T(q)是否属于(5.8.18)中的一个或另一个温度变化范围。
设cA = 107 J/m2 K, cQ = 108 J/m2 K, RA = 130 W/m2,«{}> = 120 W/m2, R(2) = 125 W/m2, Aao = 10 W/m2 K, /A = 0.5242 W/m2 K, A0 = 0.3472 W/m2 K。这些模式参数和大气(T(A} = 286 K)和海洋(T^ = 288 K)的温度观测值符合唯一稳定稳定解T[A = 286.12 K, T(q] = 288.20 K,它与经验估计只有轻微差异。大气和海洋的自主模式各自的热通量值等于Fa = F(T^\ T^) = aao(T^ - T^) = 18.78 W/m2和FQ = F(Tf \ T^) = 4o(7ou) - = 22.01 W/m2在交互模式中,一个或两个稳定稳态解:
TA = {RA + Aa0T0)I(Xa + Aao), |
To =(¿AO + + XaoRa .= l2 (5.8.23)
对于所选模型参数,所需变量TA、T0和F(TA, Tq) = Xaq(T0 - TA)分别等于295.57 K、297.94 K和23.7 W/m2。这个解决方案与最初在经验数据的帮助下发现的解决方案明显不同。因此,在海洋-大气系统相互作用模式中,解漂移是不可避免的。
我们利用了上面描述的过程。记住这个目的我们转向(5.8.16)和找到阿= F (T % \ - F (T % \ T ^) = -XA0 (T ^ - T {? >) = -2.01 W / m2, AF0 = F (T < F \ rg»)- F r (T % \ {J >) =氧化铝(r ^ u) - T™)= 1.22 W / m2。将式(5.8.17)改写为cA drA/di = RA-1ATA + aA0(T0 - Ta) - aao(7T - rg»),| 8
Co drQ/di = Ro - Ao - To - ?AO(TQ - TA) - Aao(T%> - 7f), J
然后积分。结果表明,大气和海洋在不同时刻的温度将与初始值TA] = 286.12 K, Tq> = 288.20 K完全吻合,因此交换修正过程完全排除了溶液漂移。
我们现在转向测试应用于MPI全球模型的汇率修正程序。我们首先指出它的特征。大气子模式由欧洲中期天气预报中心(ECMWF)的低分辨率谱模式表示,其中预测变量(相对涡度、速度发散、温度、比湿度、位势和地表压力)场以球面函数的有限级数形式近似表示。结果,初始方程简化为合适的方程膨胀系数只取决于时间和纵坐标。利用离散表示法得到了膨胀系数的垂直结构。采用的模型版本使用了21个球面谐波和16个垂直能级。
该模型的显著特征是引入了所谓的混合垂直坐标(c坐标与等压坐标的组合),跟踪下层下垫面的地形,并与上层等压坐标一致大气层,以及纳入“包络”地形,大致考虑到亚网格尺度下面的波动。物理过程参数化应包括的若干特征包括:首先,详细描述以相对湿度和高度为函数确定的云量;第二,考虑到辐射通量对云量、温度、比湿度和二氧化碳、臭氧和气溶胶浓度的依赖性;第三,在表层大气Monin-Obukhov相似理论和k理论的框架内,将分层对动量、热量和水分涡旋通量的影响纳入表层大气的Monin-Obukhov相似理论和k理论的范围之外,最后,确定水汽对流出现的时间,不仅取决于超绝热温度梯度的建立,而且取决于上层大尺度水汽输送发散的差异。以及大气表层涡旋水汽通量的辐散。
为了模拟海洋气候,采用了准地转模式。raybet雷竞技最新它的基础是将流速分解为正压和斜压两部分的原理。假定正压分量是立即适应的
继续阅读:Dx
这篇文章有用吗?

