洋流的水平分布
35.5 36.0 36.5
盐度(ppt)
35.5 36.0 36.5
盐度(ppt)
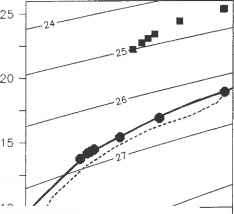
图5.3.1 (a) Iselin(1939)的T/S图显示了冬季北大西洋西部海面(开放的方格)和深度(标记为马尾藻海的实线)以及冬季北大西洋中部海面(开放的圆圈)和深度(标记为北大西洋东部的实线)的T/S关系。请注意,地表和地下的T/S关系仅在所示总温度范围的一小部分相似。(b) Williams等人(1995)绘制的北大西洋季节性变化模型的T/S图(重实线和符号)。正方形为夏季地表数据,圆形为冬季地表数据;后者直接位于同一区域的垂直T/S剖面上(实线)。类似的虚线是来自海洋气候学的T/S垂直剖面。来自Williams et al.(1995),图9。
这种大气强迫(和混合)被限制在相对较薄的海洋表层内,并消失在下面的分层水中。
蒙哥马利(1938年)是估算温跃层三维质量通量的第一个成功尝试,他构建了一个流管模型,其横向边界观察到异盐线,其上下边界观察到密度面。这条流管在上层海洋的底部有一个张开的口埃克曼层,然后沿着被观察者定义的路径盐度和密度场向下和赤道进入北大西洋主温跃层。通过这种流管的质量通量被发现大致一致的收敛埃克曼输送在流管口。Montgomery的流管模型具有区域性和诊断性,因为它需要有关示踪剂(盐度和密度)分布的详细信息,而这些示踪剂本身就是循环的结果。尽管离完整的模型还很远,蒙哥马利的流管分析仍然是建立风强迫、示踪场和三维环流之间定量联系的关键一步。
另一个至关重要的联系是温跃层循环风场由Sverdrup理论给出,该理论将经向流(海面到海底)的垂直积分直接与风应力旋度联系起来。Sverdrup关系没有区分直接由风驱动的表层和下面的地转(非强迫)流。Luyten, Pedlosky和Stommel(1983,以下简称LPS)的精液循环模型可以被看作是明确区分海洋表层(与大气直接接触,因此受到应力旋度的影响)和下面几乎非强迫(或绝热)温跃层之间的模型。Sverdrup输运关系被假定仅在温跃层内存在,温跃层水(由几个离散层表示)被假定在适当的特定纬度与大气接触。结果得到了三维环流和温跃层结构,对亚热带温跃层的主要特征有了显著的认识。特别地,LPS模型表明,由于温跃层与海面的连接(或不连接),温跃层环流可以被想象为由具有相当明显的动力学和特征路径的域组成。在直接与海面相连的区域,也就是在蒙哥马利流管内的区域,流动可以说是被风强迫的,被这样的流管扫出去的区域是“通风的”,在这种意义上,沿着这些路径之一的水在海面上是一个明确的平流,过去的时间。LPS理论对温跃层的这些通风部分进行了详细的预测,通常被称为通风温跃层模型。温跃层中还有其他广阔的区域不在蒙哥马利流管内,也没有通过逆流路径与海面相连。这些“不通风”的区域可能处于静止状态,也可能不处于静止状态; along the eastern boundary of a gyre there are extensive unventilated regions that abut the eastern boundary and extend well out into the basin (Fig. 5.3.2 is from a continuous model of the ventilated thermocline developed by Huang and Russell (1995) and having the same dynamics). These eastern regions, called 'shadow zones', have potential vorticity contours that terminate on the boundary, and so are at rest in these models. These eastern shadow zones of the LPS model appear to be analogues of the low-oxygen regions found along the eastern boundaries of most副热带环流, LPS模型对这些区域的解释是俯冲理论最令人信服的结果之一。
沿着环流的西部边界,有另一个广阔的不通风区域,可能处于活跃的环流中,尽管与大气没有直接接触(Huang和Russell, 1995,以及其中的参考文献)。在这些所谓的“池”区域内,环流通过西部边界流封闭,其细节尚未说明。由于水平混合,西池区域内的势涡度分布被假定为水平均匀的,再次需要详细说明
ISO的140°E前提条件是160'W 140"V 120"H 100°W 1英镑0"E WO"E 160"E iflO" 160只I40-W 120°W lOO' off
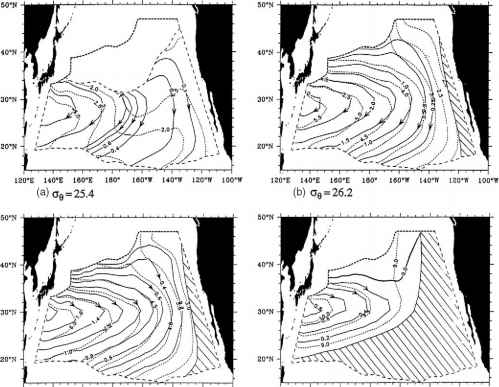
(c) ct9=26.5 (d) a9 = 27.3
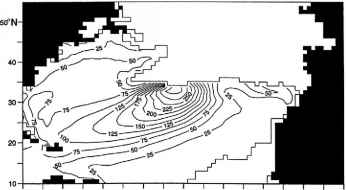
图5.3.2由Huang和Russell(1995)建立的连续通风温跃层模型计算的北太平洋四个等流面上的流型。细虚线为层深,单位为100s m。带箭头的实线为体积流函数。东部边缘的阴影区域是阴影区。Huang and Russell(1995),图7。
ISO的140°E前提条件是160'W 140"V 120"H 100°W 1英镑0"E WO"E 160"E iflO" 160只I40-W 120°W lOO' off
(c) ct9=26.5 (d) a9 = 27.3
图5.3.2由Huang和Russell(1995)建立的连续通风温跃层模型计算的北太平洋四个等流面上的流型。细虚线为层深,单位为100s m。带箭头的实线为体积流函数。东部边缘的阴影区域是阴影区。Huang and Russell(1995),图7。
不指定(只要不为零且通量向下梯度)。
在一定纬度上,Sverdrup的输送既发生在中部通风区,也发生在西部非通风池区。西部水塘区域的宽度和两个区域经向输送的比例取决于许多参数,包括风应力的分层和经向尺度的比例(亚热带的半宽度)风细胞科里奥利参数(Cori-olis parameter)的变化规模,与地球半径成正比,但依赖于纬度。这一比例可能相当小,因此在给定的等流层上,只有一小部分Sverdrup输运发生在温跃层的直接通风区域,其余都发生在西部水池区域。因此,只有一小部分海面位于蒙哥马利流管的“口”内,通常是亚热带环流的中部和东部。这一点在Iselin的作品中可能很明显俯冲图(图5.3.1a)。请注意,中心剖面(在深度和沿海面)在相当大的温度范围内非常相似,大约8°C到16°C。相比之下,西部剖面并不十分相似,在15°C至18°C范围内,西部剖面与中央剖面重叠。也就是说,西部剖面在深度上更像中央(地表或深度)剖面,而不是西部地表剖面。这表明,如果西部温跃层水起源于北大西洋海面,那么其来源则是亚热带表层的中部或东部。这种俯冲的东偏在年际海温(SST)异常的演变中具有可观察到的后果(在第5.3.4节中讨论)。
自脂多糖的开创性贡献以来,俯冲理论得到了广泛的推广和应用。本章试图对三个主要问题的进展进行总结:
表层动力学是什么俯冲过程?(5.3.2节)
连续模型(相对于分层模型)的预测是什么?LPS绝热动力学对海洋和数值模型结果的适用性如何?(5.3.3节)
3.温跃层是什么地表强迫年际变化的响应?(5.3.4节)。
黄(1991)对1990年以前的俯冲理论作了很好的回顾。Pedlosky(1996)的专著对大尺度海洋环流理论的许多方面进行了精辟的处理,特别是与俯冲有关的热带-亚热带联系,在这里讨论不多(另见Liu和Philander,第4.4章)。
5.3.2俯冲过程的表层动力学和热力学
第一种型号稳定通风thermo-cline把俯冲作为观测到的事实,然后开始寻找温跃层的Sver-drup流的结果。然而,很明显,俯冲过程(水从表层流向主温跃层的过程)必然涉及高度非绝热的上层海洋动力学和海水的综合作用环流循环.此外,关于水在哪里以及有多少水的细节也是意料之中的俯冲一定会对最终的循环产生影响,并且肯定会影响示踪剂的分布。事实上,一些观测到的大规模示踪剂库存和示踪剂年龄与Ekman泵注速率的初步比较(Sarmiento, 1983;Jenkins, 1987)揭示了一些等斜层上的俯冲速率远远超过了Ekman泵送到这些表面上的速率,这意味着俯冲过程超出了Montgomery(1938)的设想。
俯冲速率可以定义为水向下流经一个表面的速率,该表面由冬末混合层的深度定义(Cushman-Roisin, 1987;威廉姆斯,1991;马歇尔和努尔瑟,1992年;马歇尔等。, 1993)。如果这个表面是水平的,那么只有垂直速度才能支持通量,在接近海面的深处,垂直速度主要是由于埃克曼泵浦。然而,在某些地区,特别是西部边界流附近,冬季混合层深度具有明显的水平梯度,在这种情况下,纯水平速度也会将水从表层带入主温跃层,即引起俯冲。这一过程被称为“横向诱导”(Huang, 1991)。据估计,在墨西哥湾流以南和以东的地区,横向感应产生的俯冲作用与Ekman单独抽水产生的俯冲作用相当(Huang, 1990)。横向感应在北太平洋的重要性略低,因为冬季混合层深度的斜率小于北大西洋,但仍然有显著的贡献(Huang和Russell, 1995)。
晚冬混合层深度的盆地尺度倾斜本身必然是海洋与大气之间热量(或浮力)交换模式与大尺度环流相结合的反映。例如,想象一个副热带环流中的水柱。在该柱接受年平均地表加热的地区(例如北大西洋或北太平洋的东部副热带环流一般向南流动),由于热量在主温跃层上方累积,冬末混合层深度将逐年趋于浅滩(图5.3.3;森林,1985 b;Paillet和Arhan, 1996)。Marshall和Marshall(1995)、Garrett等人(1995)、Speer和tzziperman(1992)和Speer等人(1995)研究了俯冲过程的这一重要的热力学方面,Marshall等人(1999)研究了与运动学方面有关的问题。
Iselin(1939)指出的俯冲过程的一个有趣的特征是,俯冲过程明显地主要选择了晚冬的水
图5.3.3受向下埃克曼泵作用的上层海洋水柱经历季节循环的示意图。俯冲是据说发生在水从受季节影响的层进入主温跃层。在第二个冬季,混合层深度远小于第一个冬季,导致水明显俯冲到主温跃层中。如果这是一个在稳定环流中循环的水柱,我们可以把这个俯冲过程称为横向感应。来自Williams et al.(1995),图6。
俯冲。Stommel(1979)通过描述季节循环和向下的Ekman泵的影响,解释了冬季选择。在季节循环幅度较大的区域,低空内会出现暂时性的水俯冲现象季节性温跃层由于春季和初夏季节温跃层的形成(图5.3.3)。在接下来的冬天,大部分的水将再次被带入加深的冬季混合层。然而,冬季混合层的最深部分,即Ekman泵送位移大致给出的量(如果忽略其他非局部效应),将被向下推至冬季混合层的最深范围以下,并因此俯冲到主温跃层中。从而综合了上部季节循环的影响海水的密度稳定向下的埃克曼泵将从季节性温跃层(在冬末形成的水团)的最深处选择水,俯冲到主温跃层中。Williams等人(1995)已经证明,这种“斯托梅尔恶魔”选择过程在季节性变化的数值海洋模型中以非常符合斯托梅尔预期的方式运行(图5.3.1)。因此,与海面的季节周期相比,温跃层示踪场内的季节信号大大减弱。然而,温跃层内的年际变化已被检测到,并根据随时间变化的俯冲理论进行了解释(在第5.3.4节中讨论)。
5.3.3建立稳定、连续的模型:应用于数值模型分析和观测
LPS理论中的温跃层仅由几个离散层表示。虽然这种理想化的表示足以描述环流的定性特征,但更现实的连续模型更适合与观测进行密切比较(Williams, 1989,1991;Huang and Qiu, 1994;Huang和Russell, 1995)。Huang和Russell(1995)从建立在理想流体温跃层平衡基础上的连续模型开发了解析解,该模型假设密度守恒、线性化伯努利函数和主温跃层(俯冲后)内的线性化势涡。综合运输的Sverdrup关系假定为内成立
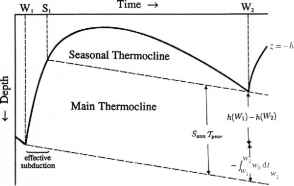
图5.3.3受向下埃克曼泵作用的上层海洋水柱经历季节循环的示意图。当水从受季节影响的层流入主温跃层时,就会发生俯冲。在第二个冬季,混合层深度远小于第一个冬季,导致水明显俯冲到主温跃层中。如果这是一个在稳定环流中循环的水柱,我们可以把这个俯冲过程称为横向感应。来自Williams et al.(1995),图6。
假定温跃层和非通风温跃层水域(第5.3.1节的水池区域)具有水平均匀的势涡度,等于通风区域内相邻流线的势涡度。表层数据包括地表密度和Ekman泵送速率。有了这个,以及其他一些详细的假设,这个问题简化为求解密度坐标下伯努利函数的自由边值问题。所得到的溶液与北太平洋温跃层(图5.3.2)具有相当惊人的相似性,并可用于诊断一些有趣的性质。首先,北太平洋由风驱动的副热带环流的深度被发现不超过约1.4公里(通常要少得多),而北大西洋的深度约为1.7公里。Huang和Russell(1995)将这种差异归因于北大西洋相对较强的热盐强迫和环流,以及在北太平洋大部分地区发现的浅而强的盐跃层(另见Talley, 1985,关于北太平洋盐度的分析)。其次,从温跃层水团的体积和对流通风量可以估算出其更新时间,其中密度最小的水团(a = 24.1 ~ 24.7)约为3年,亚热带模式水团(a = 25.3 ~ 25.7)约为10 ~ 15年。通风温跃层的质量通量主要输出到热带地区,平均而言,它必然对热带地区的温跃层性质产生重大影响(Gu和Philander, 1997;克里曼在。, 1999)。亚热带地区产生的年际异常对热带地区是否重要尚不清楚。 Third, the model yields a compact description of the mass balance of the main thermocline (Fig. 5.3.4). Within the North Pacific, the ventilated portion of the thermocline receives about 21 Sv from the seasonal layer as a result of Ekman pumping, and about 10 Sv due to lateral induction. The same figures for the North Atlantic are about 12 Sv and 12 Sv. Thus, Ekman pumping accounts for a somewhat larger fraction of the North Pacific total of subduction, a consequence of the shallow (and not strongly tilted) winter mixed-layer depth topography of the North Pacific. The meridional mass flux within the unventilated portion of the North Pacific thermocline was estimated by Huang and Russell (1995) to be about 28 Sv,
-
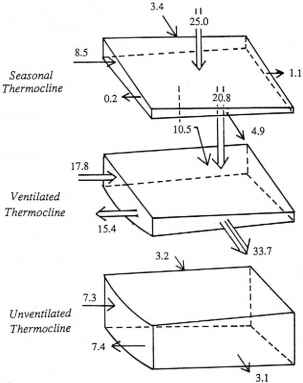
- 图5.3.4北太平洋温跃层层间的质量通量(单位为Sverdups)。北部边界是顶部,埃克曼泵浦显示为向下的双箭头。Huang and Russell(1995),图12。
约占Sverdrup运输的59%。在北大西洋,同样的数字约为42%。根据这些结果,Huang和Russell(1995)得出结论,北太平洋温跃层的通风强度低于北大西洋温跃层,这在很大程度上是北太平洋上较小的横向感应的结果。
俯冲理论提供了一种语言和概念框架,有助于描述温跃层在数值模式和海洋数据集中看到的示踪剂和环流分布。一个特别清晰和广泛的描述俯冲过程和后果的数值模式是由New et at。(1995),谁使用迈阿密等密度的模型来模拟北大西洋内的热斜深度环流。模拟是由于季节性地表场的变化而被迫进行的,经过30年的整合,温跃层环流已经接近稳定状态。中部盆地上空的等斜层在冬季到达海面(露出海面)(图5.3.5)
-
- (a) 80- W™60™40 30 20 lu 0
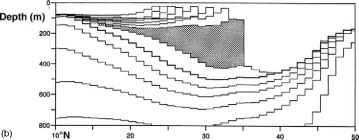
图5.3.5 (a)迈阿密等温模型密度为26.7的等温层厚度。这是整合的第30年,具有稳定的风和地面通量。这一层在细线的北面露出来。(b)冬季沿45°W的垂直剖面,阴影区为26.7层。请注意,在俯冲纬度以南(该经度约为北纬37°)的地层明显变薄。部分原因是该剖面没有与俯冲层的核心对齐,部分原因是较薄的水扩散到该层。摘自New et al.(1995),图10和11。
图5.3.5 (a)迈阿密等温模型密度为26.7的等温层厚度。这是整合的第30年,具有稳定的风和地面通量。这一层在细线的北面露出来。(b)冬季沿45°W的垂直剖面,阴影区为26.7层。请注意,在俯冲纬度以南(该经度约为北纬37°)的地层明显变薄。部分原因是该剖面没有与俯冲层的核心对齐,部分原因是较薄的水扩散到该层。摘自New et al.(1995),图10和11。
许多从LPS理论中预测到的俯冲后果。a = 26.7层上的流体被向南和向西吸入主温跃层,成为Sverdrup流的一部分。沿着它的北部,a= 26.7层与具有相同密度差的上下其他层相比具有相当大的厚度,在这方面就像一个模态水(McCartney, 1982;Siedler等人,1987;Hazeleger and Drijfhout, 1998;Schmid等人,2000年;并参见Hanawa和Talley,第5.4章)具有低位涡度(图5.3.6)。在俯冲区域下游的一段相当长的距离内,这种低势涡度(PV)形成了一个舌形,用来标记俯冲水团。(在真实的北大西洋中,没有严格可比较的模式水在这种密度和一般位置形成。)一个有趣的问题是,这一层中的水是否像理想化的LPS理论中假设的那样,保持潜在涡量。 Since the low PV tongue is surrounded by higher PV waters on all sides, there is bound to be some diffusion of (higher) PV into the subducted water mass. This significantly erodes the low PV tongue, which, 5-10 years after subduction, begins to lose its identity. The low potential vorticity is spread by diffusion into the surrounding waters, which thus have a negative potential vorticity diffusion tendency (balanced in this near steady state by horizontal advection). The change of PV within the subducted water is not small, and horizontal diffusion clearly influences the basin-scale distribution of PV (see Toole and McDougall, Chapter 5.2 for a review of mixing in the ocean). Nevertheless, the overall pattern of thermocline circulation in the numerical model solution is qualitatively as expected from the purely advective (adiabatic) theory of LPS.
在承认中尺度涡旋变率的数值模式中,俯冲速率容易受到涡旋变率的影响(Marshall, 1997),特别是在高涡能区域,例如墨西哥湾流附近的西副热带模式水的形成地点。Hazeleger和Drijfhout(2000)对墨西哥湾流区域进行了可比的涡流分解和非涡流分解模拟,以说明这一过程。净俯冲速率为
继续阅读:罗伯特·皮卡特和彼得·莱茵斯
这篇文章有用吗?

