动态分析一个简单的海因里希振荡器
在前一节中所示,之间有某种程度的一致性诊断计算7 b与7 m和观察到的海因里希事件被认为发生只有当7 b = 7 m。为了占到这些事件的quasi-cyclical进化,然而,我们必须显式地引入融化的物理过程,发生在7 b = 7米,由Eq。(9.66),在一个封闭的动力学模型。这样最简单的模型可以得到专业的PDM在12.1节制定只考虑的内部动态的冰盖用方程式表示。(12.1)、(12.3)和(12.4)(参见9.11节)。我们因此只考虑二阶变化的冰盖质量由于增兵事件,排除所有的一阶效应驱动的主要进化冰层,第15章中讨论。的反馈回路图(图第四节)我们现在只考虑循环[/世行< Si 7]排除所有其他我的链接。
特别是,萨尔兹曼和Verbitsky(1996),我们假设规模面积\占领Laurentide冰盖和堆积速率& OQ-a \ T ^约常数过去70肯塔基州,在此期间发生了海因里希清洗。然后忽略任何bedrock-calving不稳定(C \ = 0)和使用比例关系= p {\ H,我们可以写方程式。(12.1)、(12.4)和(12.3),分别以dH dt dSs dt dWB
dt的地方
Mb = - G * - ma (Mt - t *) - 7 m) + (16.7)
当结核病= 0,如果7 b < 7米;5 s = (piAi) _1 < Si(代表冰厚度损失激增的速率通量);= (piA) _1 /连续波;和th (= Vj_1) ts (= t ^ 1),和rw(=大众')是时间常数为特征冰蠕变,飙升,分别和基底排水。这些后两个时间常数只弱约束,但是合理性的争论已经由MacAyeal rs(1993)是1的肯塔基州,范·德·维恩和Oerlemans(1984),(按照基底水流的扩散近似)tw也是相同的顺序(1肯塔基州)。速率常数在Eq。(16.5),有关增兵基底液水量的变化,更是弱约束。我们认为rs, rw,,必须以某种形式出现在所有型号的冰盖不断飙升,将自由参数被确定为一组(nonunique)的预测值需要解释观察到的变化(在我们的例子中海因里希振荡)。关闭系统,我们必须添加公式、方程式。(16.1)和(16.3),7 b和7米。反馈回路原理图显示的主要变量的周期性耦合模型在图16-6。
可能认识到冰体积V (H),增兵损失(8 s)和基底水量(Wb)的主要变量描述的更复杂的模型Oerlemans (1982 b),他展示了振荡行为的可能性,尽管更长的时间尺度(100肯塔基州)比海因里希事件(10肯塔基州)。为了说明我们目前的可能性更简单的系统可以表现出波动的
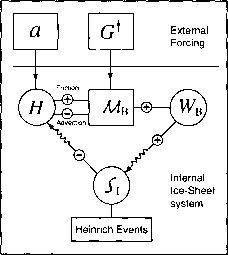
图16-6反馈回路原理图模型系统(方程式。(16.4)-(16.7)]显示内部的高度之间的耦合的冰盖(H),基底水深(Wb)和飙升的冰层厚度损失(Si)的影响下不断迫使由于净雪积累(a)和地热通量(Gt)。
图16-6反馈回路原理图模型系统(方程式。(16.4)-(16.7)]显示内部的高度之间的耦合的冰盖(H),基底水深(Wb)和飙升的冰层厚度损失(Si)的影响下不断迫使由于净雪积累(a)和地热通量(Gt)。
海因里希的时间尺度,我们采取以下合理的物理常数的值和参数:p;n = 3 = 917 kgm ~ 3日,g = 9.8 ~ 2女士,c = 2 x 103 Jkg_1 /°c, k = 10 ~ 6 m2 s_1, c = 0.04 Wm ~ 2, y = 10”2“厘米”1,和一个= Ucmy " 1(堆积速率较低的中部地区的冰盖的特点,我们认为冰轨迹,提供表面温度7 h底部,产生),和th = 50肯塔基州。我们分配的多个弱约束参数值的设定,肯塔基州rs = rw = 1.5, = 10 ~ 5 y ~ 2。
图中所示的解决方案是16-7从任意初始条件。我们注意到大约14-ky时期发生的振荡,特点是滞后变化7 H, 7 b, 7 b, H, < Si赞同(融化。Mb > 0)当7 b = 7 m -结果不定性改变为小参数的变化。
50 100 150 200 0
50 100 150 200 0
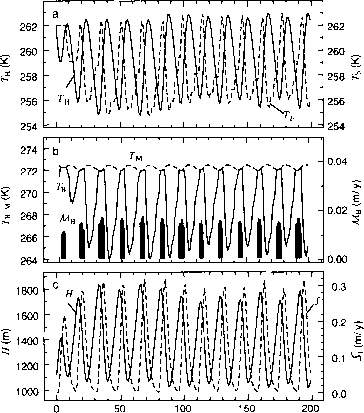
图16-7时变动力系统的解决方案,显示(a)上表面温度的波动(7 h)和温度在z = Zb (Tb)、(t >)压力融化点(7米),基底温度(7 b)基底融化黑条率(Mb),在底部面板增兵放电单元的冰厚度损失(Si)和冰盖厚度H。
图16-7时变动力系统的解决方案,显示(a)上表面温度的波动(7 H)和温度在z = Zb (Tb)、(t >)熔点(7米)的压力,基底温度(7 b),基底融化率(Mb),黑色的酒吧,和在底部面板增兵放电单元的冰厚度损失(Si)和冰盖厚度H。
因此,使用一个基于基本热力学性质的冰盖动态模型,我们表明,这样一个模型可以表现出周期性波动的大致规模一样观察海因里希事件。在其最简单的形式,这种模型提供必要的物理过程耦合变化的管理冰体积,意味着基底水量,和冰的激增,暴露出明显的自由参数可能会出现在任何更详细的模型。系统主要由内部热力学过程的影响在冰层与基底摩擦加热,产生的不稳定是由冷平流上冰面和弱得多的影响地热供暖。在这方面,涉及的机制类似于Oerleman (1982 b)的模型,但只有MacAyeal放电阶段的(1993)binge-purge模型。
很明显,很多改进和扩展可以使这个简单的模型,其中一些是显而易见的:
1。使堆积速率(a)一个变量依赖于气候(例如,SST)改变迫使海因里希的事件。这应该包括考虑气流的变化由于高度的冰盖的变化和治疗温盐环流的变化如讨论Birchfield(1989),主料和Labeyrie(1994),主料(1995),和Seidov杂粮面包(1999)。因此,反馈的图,图。第四节,新-之间的链接应该添加< Sj£和年代,f。
2。考虑,更多的观察和理论的细节,隐含基底排水过程所暗示的风化层变形的作用,和更详细的过程参与冰stream-ice货架动力学(见第9章)。
3所示。这些H-events动态耦合的主要长期进化冰层一方面,和更高的频率D-0类型的事件(例如,债券周期所示图3-7b)另一方面(见,例如,主料,1995)。
在下一节中,我们讨论这些更高的千禧年的振荡频率。
继续阅读:参考书目
这篇文章有用吗?