涡旋与层流环流模式及其应用

伯纳德·巴尼耶，蒂埃里·彭德夫和克洛西德·朗莱

摘要中尺度涡旋是海洋环流中普遍存在的、非常活跃的特征。它们在用于的高分辨率模型中表示海洋预报但在今天气候系统模型的层流、粗分辨率海洋组件中还没有。raybet雷竞技最新然而，高性能计算的进步很可能在不久的将来改变这一点，因为在下一个十年，在地球系统建模的更广泛背景下，涡流模型的使用应该会越来越频繁。本讲座讨论不同分辨率模型中的中尺度涡。课程安排如下。第10.1节通过卫星观测中普遍存在的海洋涡旋的说明，介绍了中尺度涡旋的概念。然后，通过与大气天气涡旋的类比，给出了海洋中尺度涡旋的定义。回顾了海洋中尺度涡对大气环流的主要影响。第10.2节讨论了将原始方程与分辨率、参数化和数值联系起来的一些海洋模式基础。讨论了网格分辨率的选择所导致的已分辨尺度和未分辨尺度之间的分离，给出了涡旋和层流分辨率模型的定义，并以中尺度涡旋为例说明了亚网格尺度参数化的概念。第10.3节说明了存在于分辨率和数值之间的紧密联系。 Examples are shown where the use of advanced numerical schemes improves model solutions in a more drastic way than increases in resolution. Section 10.4 uses the DRAKKAR hierarchy of全球海洋环流模型(其分辨率在2和1/12°之间变化)，以说明分辨率的变化如何影响模型模拟的真实性，就平均状态和可变性而言。结论部分总结了课堂上讨论的主要内容。

实验室Géophysiques和工业，国家科学研究中心，Université约瑟夫傅里叶e-mail:(电子邮件保护)

A.席勒、G. B.布拉辛顿主编，操作海洋学在21世纪，239

DOI 10.1007/978-94-007-0332-2_10，©施普林格Science+Business Media B.V. 2011

10.1介绍

本课程讨论海洋环流数值模式的分辨率问题，更具体地说，是这些模式对中尺度涡旋的表示。因此，本讲座将区分两类模型。一类模型使用“粗分辨率”网格，产生的解决方案以“层流”动力体系为特征，其中中尺度涡无法出现。另一类模型使用“高分辨率”网格，所产生的解决方案以“涡流”为特征，其中中尺度涡流可以出现和发展。本文用“层流”和“涡流”来限定模型所产生的流动的动力区，而用“粗”和“高”来标记数值网格的分辨率。

10.1.1海洋中无处不在的涡流

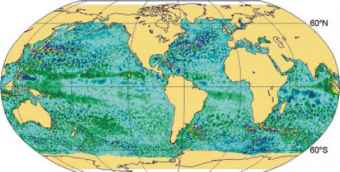
的普遍性海洋里的涡流已被大量使用卫星(如测高仪，见Chelton et al. 2007)和原位仪器的研究所证实。图10.1a显示2004年5月19日卫星测高观测到的海平面异常。这片海洋看起来充满了几百公里大小的特征。这些观察到的特征通常存在几天到几个月，有些特征持续两年以上(Chelton et al. 2007)。

虽然大气和地形的影响也发挥了作用，但这些涡流被认为主要是由主要洋流的不稳定性产生的;这解释了为什么在边界流及其近海延伸(如墨西哥湾流、黑潮)和南极绕极流附近发现了更集中的强中尺度特征。这些特征在中央也无处不在副热带环流以及在中纬度海洋盆地的东部(也容易发生动力不稳定)。中尺度涡旋也沿赤道产生(它们明显更大，而且往往更各向异性)和在海洋内部产生(靠近地形障碍，或通过剪切不稳定等)。简而言之，现代观测揭示了一个“中尺度涡的海洋”，其一般特征与更大尺度的环流模式有关，并被各向异性增强的较小(所谓亚中尺度)动力结构所分离。

10.1.2海洋中尺度涡的定义

海洋中尺度变异性以各种瞬时特征出现，如漩涡、蜿蜒空间尺度为10 ~ 100公里，时间尺度为10 ~ 100天。海洋漩涡主要大尺度水流系统的水动力不稳定性自发产生

3卫星高度测量(Aviso!

240* w 120'w ot

3卫星高度测量(Aviso!

240* w 120'w ot

24q°w 120* w o 'e

■0 5 -0.4 -0.3 -0.2 -0.1 0.0 0.1 0.2 0.3 0.4 0.5米

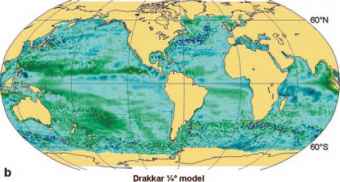
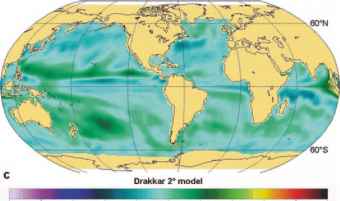
图10.1 2004年5月19日的海平面异常(米)，(a)卫星测高(Aviso产品)观测到的海平面异常，以及(b) 1/4°允许涡流的全球模型(Drakkar模型ORCA025，运行序列G70)和(c) 2°粗分辨率全球模型(Drakkar模型ORCA2，运行序列G70)模拟的海平面异常。这两个模型使用相同的数值代码(NEMO)和相同的大气强迫(DFS3，见文本)。

■0 5 -0.4 -0.3 -0.2 -0.1 0.0 0.1 0.2 0.3 0.4 0.5米

图10.1 2004年5月19日的海平面异常(米)，(a)卫星测高(Aviso产品)观测到的海平面异常，以及(b) 1/4°允许涡流的全球模型(Drakkar模型ORCA025，运行序列G70)和(c) 2°粗分辨率全球模型(Drakkar模型ORCA2，运行序列G70)模拟的海平面异常。这两个模型使用相同的数值代码(NEMO)和相同的大气强迫(DFS3，见文本)。

大尺度不稳定的大气天气特征风系统．海洋中尺度涡经常被描述为全球海洋的“天气系统”，在动力学上与大气的天气特征类似(McWilliams 2008)。

让我们考虑一个海洋或大气流动在垂直分层的流体中。垂直分层的特征为Brunt-Vaïsala频率N:

H阿宝

H为平均流垂直切变的特征尺度(如海洋厚度)主要温跃层或者大气对流层高度)， p0为参考密度，Ap为堆积密度梯度除以H, g为重力加速度。

设U为涡旋特征速度尺度，L为涡旋特征水平尺度，f为科里奥利参数。动态地，海洋中尺度(和大气天气)涡可以定义为以下特征:

•处于准地转平衡(即较小的罗斯比数):

•与(内部)重力波的速度相比，具有较小的特征速度(即较小的弗劳德数):

U U Ap

Fr = ^Fj = NH«1 with g' = gAP (10.3)

VgH NH Po

•是由大尺度流动的不稳定性产生的，因此，同样受到分层和旋转的影响(即order 1 Burger number):

*=f=(f)2=0 <"

由式b = 1可以很容易地估计出特征涡旋水平尺度为:

N= 10-2 s-1和H= 104 m的典型大气值产生了Latm = 1,000 km的中纬度(即f= 10-4 s-1)天气性涡旋长度尺度。典型海洋值N= 5 × 10-3 s-1, H= 103 m，产生的中尺度涡旋长度尺度Loe=50 km。因此，在海洋中，典型的涡旋长度尺度要小20倍。

在这两种流体中，这些涡流对全球环流的动力影响可能是非常不同的，至少在数量上是不同的，海洋和大气涡流之间的类比可能在这个尺度分析之后就不成立了。例如，很明显，由于大气涡流的大小要大得多，它在将热量从亚热带输送到亚极地纬度方面的效率要高得多。事实上，大气天气涡旋几乎要对整个过程负责向极地的热输送从30°到60°纬度，以及在大气环流模式中解决这些特征的必要性从未受到质疑。

海洋漩涡的尺寸越小，就意味着向极地输送热量(和盐)的效果越弱，特别是在地球的大部分地区经向热传输(至少在北半球海洋的部分地区)是由沿大陆向极地流动的平均洋流完成的(大陆允许海洋中强的、局部的地带性压力梯度在地球上与向极地的边界流保持平衡)。虽然涡流传输的重要性已得到承认，但在海洋环流模式(ogcm)中解决涡流的必要性仍存在争议，用于气候预测的模式仍然是层流的，即使用粗分辨率网格，依靠参数化来解释更大尺度中尺度涡流的影响。raybet雷竞技最新

10.1.3中尺度涡的重要性

涡流是海洋中普遍存在的特征，它包含了海洋中很大一部分动能。与大气天气系统类似，它们的能量传输对全球范围内环流的动态平衡至关重要。它们之所以重要，是因为它们对大尺度环流有反馈，并对海洋总热通量有重大贡献。涡流过程对强洋流和锋以及水团物理和生物地球化学性质的产生和维持也有重要影响，因为它们是海气交换、等流扩散和混合、密度再分层、通风和俯冲、能量级联和耗散、地形形式应力等的主要参与者(mcwill -liams 2008)。涡流也是内在气候变率的来源。raybet雷竞技最新它们对海洋生态系统有很大的影响，对海洋安全、污染扩散、近海工业、渔业等海洋业务应用非常重要。

10.2海洋模式中的一些分辨率问题10.2.1已解决和未解决的运动尺度

海洋模型的基本原理最近在一系列论文中被彻底重新审视(Griffies 2004;Griffies et al. 2005;Treguier 2006;Griffies和Adcroft 2008)。本课程主要讨论解析度问题，有关海洋环流数值模型中所用的方程和数值算法的更多内容，读者可参考上述论文。海洋环流模型通常求解所谓的原始方程(Madec 2008;例如)，它是Navier-Stokes方程的近似值，以及将两个活性示踪剂(温度T和盐度S)与密度p耦合的非线性状态方程。

基于尺度考虑，最重要的假设是(i)薄壳(或浅水)近似(海洋深度比地球半径小得多)，(ii) Boussinesq近似(密度变化被忽略，除非它们对浮力的贡献)，(iii)流体静力假设(垂直动量方程被简化为浮力和浮力之间的平衡垂直压力梯度)和(iv)不可压缩性假设(三维速度矢量不发散)。

为了本课程的目的，原始方程(PEs)被写成(Treguier 2006):

dt u = (u, v, w)是三维速度向量，Y = (u, T, S)是海洋的预测连续状态向量，F(Y)包括PEs的所有其他项，包括科里奥利力，和压力梯度力、外力等。由于本讲座侧重于中尺度涡，因此应考虑(10.6)中的F(Y)项还包括由小尺度三维湍流诱导的双涡混合的参数化(见(Large et al. 1994;大型1998年)的小规模审查湍流闭合模型)。原始方程的更标准的形式在附录中给出。

式(10.6)是数值求解的，这意味着PEs在网格上使用有限差分格式(或其他数值方法)进行离散化。数值求解PEs意味着对状态向量Y及其演化方程(10.6)应用“离散化”算子()R，得到:

^ + (u -VY)r + (F(Y))r = 0(1°.7)

其中，YR=(Y)R是模型解(即海洋状态的离散表示)。根据Treguier(2006)，(10.7)可以改写为:

^ +你的■VYr + Fr(年)= - ((u■v) r - ur■VYr) - ((F (Y)) r - Fr(年))

解析尺度对海洋解析状态影响的演化方程海洋解析状态

数值模型在时间上进行积分(10.8)，在大于网格步长和离散时间的空间尺度上提供了YR(海洋的离散状态)的连续值。请注意，离散状态(10.8)的演化方程的左手边与连续状态(10.6)相同，但右手边(RHS)有额外的贡献，表示未解析尺度对已解析模型解的影响。已解决和未解决尺度的定义涉及平均算子(Griffies 2004)。RHS术语(10.8)通常是未知的。模型中用于计算这一项的解决方案通常包含经验关系或基于物理的模型(即参数化或亚网格尺度模型)。这些模型表达了未解决过程对已解决状态的贡献，遵循类似于“湍流闭合假设”的方法，该方法产生高阶矩作为低阶矩的函数(Lesieur 2008)。

10.2.2涡流与层流海洋模型

选择海洋环流模型(OGCM)的网格分辨率在形式上相当于选择一个适当的平均算子(网格步骤的低通滤波)和一个适当的方法来估计较小尺度的贡献(即RHS为(10.8))。如果操作员()R雷诺兹算子的性质,即如果没有解决(或subgridscale)海洋状态向量Y的一部分,定义为Y = Y-YR验证(Y) R = 0(如果流验证属性的平稳性和遍历性,看到(Lesieur 2008详情),然后悬而未决的部分,对应于非线性平流的影响(即第一项的RSH(10.8)),可以表达的形式涡通量散度:

((u■VY)r - uR■VYr) = V■(u' y ') r (10.9)

在本课程中，我们不讨论(10.8)RHS的第二项的处理，其中包括未解决的但仍然重要的强迫效应。在下面，我们假设它包含在术语FR(YR)中。离散模型式(10.8)为:

BYr dt

+ UR■VYr + Fr (Yr) = -V(u' y ')r (I0.I0)

(10.10)的RHS(即“雷诺应力”，如果Y是动量，和湍流热通量如果Y是位温)是涡流参数化的问题。

当选择一个模型的分辨率时，人们必须回答这样一个问题，即应该明确地模拟哪种“涡流效应”来解决给定的科学问题。例如，人们期望不同的答案来预测短期内的洋流和锋面(在这种情况下，涡流应该明确地解决，需要精细的、计算成本高的网格)，或者模拟海洋经向热输送的几十年变化(在这种情况下，涡流效应可以参数化在粗糙的、计算效率高的网格上)。

纬度

图10.2全球模型Drakkar层次中水平网格分辨率(km)随纬度的变化(分辨率从2到1/4°)。绿色虚线表示第一变形半径的变化(~涡长尺度)。全黑线(虚线)显示了计算网格在子午(纬向)方向上的大小。粗分辨率模型(2°、1°和1/2°)的经向网格仅比赤道带的涡旋尺度更细(2°和1°网格的局部经向细化)。1/4°(涡流)模型的网格比40°N和40°S之间的第一变形半径更细。一个在所有纬度的“涡旋解析”模型的目标应该是在赤道处达到10公里或更好的分辨率。这几乎是通过正在开发的1/12°Drakkar模型配置获得的(改编自Penduff等人，2010年)

纬度

图10.2全球模型Drakkar层次中水平网格分辨率(km)随纬度的变化(分辨率从2到1/4°)。绿色虚线表示第一变形半径的变化(~涡长尺度)。全黑线(虚线)显示了计算网格在子午(纬向)方向上的大小。粗分辨率模型(2°、1°和1/2°)的经向网格仅比赤道带的涡旋尺度更细(2°和1°网格的局部经向细化)。1/4°(涡流)模型的网格比40°N和40°S之间的第一变形半径更细。一个在所有纬度的“涡旋解析”模型的目标应该是在赤道处达到10公里或更好的分辨率。这几乎是通过正在开发的1/12°Drakkar模型配置获得的(改编自Penduff等人，2010年)

如果使用，模型将会“旋转”

•水平网格，其分辨率足以让中尺度动力学出现，即斜压和正压不稳定过程被明确(尽管是部分)解决;

•未解决(较小)尺度对已解决(中尺度)特征的影响的适当表示。

在实践中，这意味着网格网格要比涡旋长度尺度更细(见图10.2，对于涡旋尺度(10.5)为50千米，网格网格通常为10千米量级或更细)。未解尺度对中尺度动力学的影响通常通过高粘度(例如双谐)参数化，这种方法确保了数值稳定性，但在物理上并不完全令人满意。研究正在进行中，以开发更一致的替代方案(例如Frisch等，2008年)。一个模型将是“层流”如果它使用

•粗糙的水平网格，其分辨率不让中尺度特征出现;

中尺度特征对分辨率(例如盆地尺度)特征的影响的适当表示。

在实践中，这意味着要有一个比涡长度尺度更宽松的网格(见图10.2，对于50公里的涡尺度(5)，通常是50-100公里量级的网格)。在粗分辨率建模中，中尺度尺度对大尺度动力学的影响依赖于参数化，这些参数化可以同时解释中尺度涡的扩散和平流效应。

请注意，在“旋涡”和“层流”模型中，在时间上的积分是相同的Eq.(10.10)，但在每种情况下，未解析特征具有不同的空间尺度:它们对已解析尺度的影响必须在两类模型中由不同的参数化表示(打开模型发展的两种不同方式)。下一节将介绍在层流模型中广泛使用的中尺度涡的参数化。

10.2.3层流模式中尺度涡的参数化

中尺度涡旋对大尺度海洋环流影响的表征是用于模拟气候系统的海洋模式的一个关键问题。raybet雷竞技最新正如我们在引言中提到的，这些影响是多方面的。然而，没有参数化可以解释所有的涡，中尺度涡的参数化是基础研究的一个活跃领域(Eden and Greatbatch 2008;Zhao和Vallis 2008)。

在所有涡旋特性中，中尺度涡旋沿等流表面混合示踪剂的能力对大尺度上的密度和示踪剂分布影响最大，必须在粗分辨率海洋气候模型中参数化。raybet雷竞技最新在本课程中，我们将讨论模拟这种效果的经典方法。将势温T写成(10.10)可得:

dtR + uR■VTr = -V■(uT')R + Dt + Ft

与课程中使用的符号一致，TR和uR=(uR, vR, wR)是位温和当前的速度因此，(u' t’)R表示未解的(中尺度)热涡流通量，必须估计其散度才能关闭方程。术语DT和FT表示双流通量和强迫(FR(YR)项为(10.10))。

将中尺度涡旋通量参数化意味着用一个基于物理的理论模型来阐明它们对模型解TR的影响。该模型通常是由涡动通量(u' t)R与分辨率尺度VTR梯度之间的关系构成。这个关系可以正式地写成张量形式如下:

z是混合张量，x,y,z表示主要的混合方向(为了简单起见，这里是坐标系的主轴)。继Müller(2006)之后，

混合张量被分割成一个对称的部分，K.，反对称部分S…

V V

这样(10.12)写为:

仍然遵循Müller(2006)，对称张量K..通量散度可以用拉普拉斯热扩散(K7ATr)的形式表示，而反对称(或斜)张量s的通量散度可以用斜(或圆)速度向量V* (-V*VTR)表示为简单的热平流。涡动通量散度(10.12)可写成:

-V(uT')R = KtATr -V *•VTr (10.14)

中尺度涡旋通量参数化的挑战随后被简化为KT(湍流扩散系数)和V*丸速的确定。

在海洋模型的实践中，拉普拉斯热扩散(RHS(10.14)中的第一项)仅作用于等流表面(Redi 1982)，以解释由中尺度涡造成的内部等流混合。在小尺度三维湍流引起的垂直混合作用面前，其对底轴方向的贡献被忽略。扩散系数KT的值通常取决于用户和应用，并可能受到数值稳定性考虑的约束。(10.14)中RHS第二项的表达式由GM90参数化(Gent和McWilliams 1990)提供，该参数化模拟了热的(未解决的)涡流平流对已解决的(大尺度)浮力场的影响。该参数化使用局部等视斜率来定义三维非发散丸速度V*=(u*， V*， w*)，形式如下:

其中pR为解析密度场。V*的作用是从大尺度流中释放势能，其物理方式与斜压不稳定所产生的中尺度涡压平等斜线的方式一致，即从平均流中提取势能。换句话说，涡诱导等流层厚度沿等流面向下梯度扩散，扩散系数为K*。

综上所述，用GM90涡流参数化求解的温度方程有以下形式(盐度同样适用):

Ap表示沿(Redi 1982)定义的局部等视面作用的二维拉普拉斯算子。(10.16)中的所有项现在都表示为解析变量TR和uR的函数，涡流效应由拉普拉斯扩散项和丸速项解释。后两个术语都是在物理假设下推导出来的，即涡流沿等旋面混合性质，并已使用混合张量的数学形式表示。密度场上涡动通量的参数化随后简化为温度和厚度扩散系数KT和K*的确定。这些系数的评估仍然部分是经验的。在粗分辨率模拟中，GM90参数化已被证明能显著改善大尺度密度场和环流，是海洋气候模式中使用最广泛的中尺度涡参数化。raybet雷竞技最新

10.3高级数值格式和解析

虽然GM90参数化及其变异演化是粗分辨率模型的公认改进，但许多涡流效应尚未在这些模型中得到考虑。此外，越来越多的海洋模式应用需要明确的中尺度涡旋分辨率，特别是在海洋预报中。因此，涡流模型的使用正在迅速增长。但是提高分辨率并不像增加网格网格那么简单。随着分辨率的提高，在模型解中出现更精细的空间和时间尺度，亚网格尺度参数化需要演变(因为它们必须考虑到不同未解决的物理过程的影响，例如涡流模型的亚中尺度效应)。用于求解方程的数值算法可能也需要适应新的物理过程，尽管问题的公式没有改变。这后一个方面，链接分辨率和数字是在这一部分的课程与动量平流方案说明。pe的动量方程，以标准形式写成(注释见附录)为:

+ (u - v)u - fv =——+ Du + Fu(1°.17a)

Dt Po dx

经向动量dv 1 dP先生。

- + (u - v)v + f u =——+ Dv + Fv (10.17b)

Dt Po dy

(10.17)中的(u- v)u和(u- v)v项是表示动量平流的非线性项。有各种各样的数值方案来计算有限差分中的这些项，我们在这里说明了它们对数值模型的解的影响。

我们正在比较三种不同的二阶平流方案对使用NEMO OGCM的涡流允许(1/4°)模型解的影响

(Madec 2008)。方案(在(Le Sommer et al. 2009)中详细介绍)具有不同的数学公式，下面将简要介绍:

•EFX方案:以通量散度的形式书写，该方案是节能的。

•ENS方案:以动能梯度和涡度项的形式写成，该方案是熵守恒的。

•EEN方案:也写在动能梯度和涡量项的形式，它使用比ens更大的模板。该方案是能量和能量守恒。

对这些平流方案的敏感性实验已经使用Drakkar模型配置(基于NEMO OGCM (Madec 2008)，见章节10.4)进行。粗分辨率(层流)配置(2°或1°)对方案选择的敏感性较弱，正如预期的那样，(u-V)w项在大尺度(非常小的罗斯比数)的贡献很小。然而，涡流允许配置(1/4°)被证明对这种选择非常敏感，如图10.3所示。模拟的平均环流在强流区域的模式和振幅上有显著的改变。例如，与ENS方案相比，EEN方案显著地向南偏移了墨西哥湾流(图10.3)。

由(Le Sommer et al. 2009)证明，与其他两种方案相比，EEN方案可以降低底部单元附近垂直速度场的噪声。平均电流连续性增强和地形整流效应增强也被EEN方案诊断出来。这可能有助于改善西部边界流，并显著减少哈特拉斯角的惯性涡流(另见Barnier et al. 2006;Penduff et al. 2007)。

动量平流方案也发现影响轨迹Agulhas戒指在本格拉盆地(Barnier et al. 2006)。在一些涡流模型中，包括POP模型(1/10°)和带有ens的1/4°Drakkar模型，这些轨迹往往是伪直的、确定的和不变的。在1/4°Drakkar模型中使用EEN方案大大减少了这种广泛发现的不一致性，产生了更真实的(即更混乱和不规则)南大西洋的环脱环事件和轨迹，如涡流动能模式所示(图10.4)。其他例子(Barnier et al. 2006;Penduff et al. 2007)证实，使用高级数值格式(例如在z坐标模型中使用地形的部分阶跃表示)可能以比提高分辨率更显著的方式改善模型解。

10.4分辨率对模型解的影响

在课程的这一部分，我们使用全球海洋环流模型的Drakkar层次结构，其分辨率从2到1/12°，以说明分辨率的变化如何影响模型模拟的真实性。

正压输送在EEN和ENS之间的差异

1 207 413 619 824 1030 1236 1442

■70 -60 -50 -40 -30 -20 -10 0 10 20 30 40 50 60 70 Sv

图10.3用0RCA025(1/4°)Drakkar模式模拟的两次平均正压流函数的差异。一个模拟是使用EEN动量平流方案和它的双胞胎是使用ENS动量平流方案(差异EEN减ENS显示)。较大的差异(即大于±10 Sv)仅在强非线性电流区域发现

10.4.1模型配置DRAKKAR层次结构

Drakkar是一个合作组织，它汇集了欧洲几个研究和业务海洋学小组的资源和专业知识，目的是开发、共享和改进可用于研究和业务应用的全球海洋/海冰模型配置的层次结构(Drakkar Group 2007)。Drakkar使用了NEMO建模系统(Madec 2008)1和AGRIF网格细化软件

1 NEMO包括一个海洋模型、一个海冰模型和一个模拟地球化学被动示踪剂(即14C、CFC11、SF6)演化的模块。

图10.4南非周围的平均地表涡旋动能(每平方厘米秒2)，(a)卫星测高观测(Ducet et al. 2000)，以及(b) EEN方案的全球0RCA025 Drakkar模式、(c)全球P0P1/10°全球模式和(d) ENS方案的全球0RCA025 Drakkar模式模拟的结果。所有模型结果都显示了3年以上计算的速度方差

图10.4南非周围的平均地表涡旋动能(每平方厘米秒2)，(a)卫星测高观测(Ducet et al. 2000)，以及(b) EEN方案的全球0RCA025 Drakkar模式、(c)全球P0P1/10°全球模式和(d) ENS方案的全球0RCA025 Drakkar模式模拟的结果。所有模型结果都显示了3年以上计算的速度方差

图10.5 DRAKKAR 0RCA025构型的三极网格(赤道分辨率为1/4°)，每12点绘制一个点(总共1442 x 1021个网格点)。这种涡流允许配置被MERCATOR-Ocean用于业务预报

图10.5 DRAKKAR 0RCA025构型的三极网格(赤道分辨率为1/4°)，每12点绘制一个点(总共1442 x 1021个网格点)。这种涡流允许配置被MERCATOR-Ocean用于业务预报

ware (Debreu et al. 2008)Drakkar也为NEMO的持续发展做出了贡献。

Drakkar使用三极ORCA网格实现了全球和区域NEMO配置的层次结构(Madec和Imbard 1996)，(图10.5)。在2,1,1 /2,1/4和1/12°水平分辨率下进行了全局模拟。每个配置都使用域分解(最多1000个处理器)在大型并行计算机上运行。模型层次结构的主要特征如表10.1所示。1/4°ORCA025结构和模型层次的详细描述分别见于(Barnier et al. 2006)和(Penduff et al. 2010)。

在强迫函数中使用的体公式是由(Large和Yeager 2004)提出的。Drakkar模拟中使用的大气强迫场来自CORE数据集(Large和Yeager 2008)，以及Drakkar强迫集DFS3或DFS4 (Brodeau et al. 2010)。DFS强迫采用ERA40 6小时地表大气变量计算湍流通量(风应力,潜热与感热通量，蒸发)，每日卫星辐射通量(向下短波和长波)和卫星估计的月降水量。(Brodeau et al. 2010)描述了应用于这些数据的各种修正。请注意，最近的发展介绍了太阳辐射的日周期和海洋生物学对深度依赖的贡献光吸收．大多数Drakkar模拟涵盖了1958-2004年期间(Drakkar Group 2007)。

2参见(Biastoch et al. 2008)在Agulhas反流地区应用AGRIF的例子，参见(Chanut et al. 2008)在拉布拉多海的应用，或参见(Jouanno et al. 2008)在加勒比海的应用。

表10.1全球模型配置Drakkar层次结构海洋分量的主要设置这里不描述LIM2海冰模型的设定(Fichefet et al. 1997)

46到75层垂直高度	地形	平流方案
地面:6m ~ 1m底部:250m ~ 200m	部分步骤	动量:EEN示踪剂:FCT
水平混合2°-l°模型	1/2的1/4°	模型的特殊性

水平la placían K，=4xlOJto lxloVV

等旋lap lac i Kt= 1000 mV涡流GM90

参数化K. - 2000至1000 mV'

动力

T,S，示踪剂水平平行

Kv = 12x10"电网依赖

1.5x10" mV等视层紫胶

电网的依赖

没有一个

垂直混合	T, S，示踪剂	动力	特殊性
背景	Kf =值列表/ s	K = 10 J m Vs	(l()’海冰下fl)
动荡的关闭	TKE方案	TKE方案	破波和朗缪尔钟的参数化
对流	K。= 10 mV	K = 10mv	增强垂直扩散

边界条件	侧墙	底	表面
参数化	free-slip	二次阻力定律(C " = I05)	熔剂形式-散装公式
特殊性	2l处没有滑倒	内部潮汐混合扩散和平动BBL	-核心强迫 —DFS强制集 -表面盐度松弛

本课程中使用的大多数模拟都来自G70系列，其中2,1,1 /2和1/4°Drakkar模型在1958-2007年的50年期间由DFS3强迫驱动。

这些模拟与2个观测参考资料进行了比较:现场EN-ACT-ENSEMBLES水文数据库(EN3-v2a, Ingleby and Huddleston 2007)和AVISO高度计(SLA)数据库。为此，一种基于空间和时间四线性插值方案的搭配算法以与观测完全相同的方式对模型输出进行子抽样;然后使用专用指标来比较观察到的和模拟的配置数据库(见图10.6)。

sdiinhy偏见

图10.6 DFS3强迫驱动的0RCA025 Drakkar模拟(运行序列G70)中模型温度(上)和盐度(下)偏差(相对于2000-2004年期间)的垂直结构。参考数据是EN3-v2a水文数据集。彩色是温度和盐度偏差(x轴)作为深度(y轴)函数的pdf(对数尺度)。这些依赖深度的pdf的中位数(绿线)和模态(白线)是叠加的(M. Juza et al. 2011，个人交流)

sdiinhy偏见

图10.6 DFS3强迫驱动的0RCA025 Drakkar模拟(运行序列G70)中模型温度(上)和盐度(下)偏差(相对于2000-2004年期间)的垂直结构。参考数据是EN3-v2a水文数据集。彩色是温度和盐度偏差(x轴)作为深度(y轴)函数的pdf(对数尺度)。这些依赖深度的pdf的中位数(绿线)和模态(白线)是叠加的(M. Juza et al. 2011，个人交流)

10.4.2分辨率增加的部分影响

事实证明，德拉卡尔模型层次在评估网格分辨率对与气候相关的海洋环流特征表示的影响方面非常有用。raybet雷竞技最新图10.1a显示2004年5月全球海平面异常平均一周的高度计观测，具有强烈的中尺度涡旋特征。这些中尺度特征在2°时明显不存在(图10.1c)，但在1/4°时清晰可见，并呈现出真实的模式(图10.1b):从这个中尺度角度来看，层流和涡流海洋模型并不能模拟“相同”的海洋。比较这两类模式更有趣，也更有意义，重点是这两类模式所捕捉到的相对大规模的特征，如流域尺度综合气候指数、空间平滑平均水平环流和年际变率(LSIV)模式。raybet雷竞技最新

图10.7在相同DFS3强迫的驱动下(运行序列G70)，在增加分辨率(2,1,1 /2和1/4°)的4次Drakkar模拟中获得的大西洋平均经向倾覆流函数。等高线间隔为2 Sv (Lecointre 2009)

图10.7在相同DFS3强迫的驱动下(运行序列G70)，在增加分辨率(2,1,1 /2和1/4°)的4次Drakkar模拟中获得的大西洋平均经向倾覆流函数。等高线间隔为2 Sv (Lecointre 2009)

经向翻转环流(MOC)和经向热输送(MHT)对分辨率变化具有一定的敏感性。大西洋MOC的经向结构从2°到1/4°几乎没有变化(图10.7)，MOC和MHT的平均振幅增加了约25%(表10.2)。

然而，MOC的低频变率(图10.8)在所有模拟中非常相似:尽管其他气候指标可能存在显著差异，但这一结果表明，涡流模式在模拟MOC和MHT的缓慢演化时可能不会产生重大变化。

表10.2在相同的DFS3强迫驱动下，Drakkar层次的各种模型估算的大西洋MOC和MHT在26°N

决议大西洋MOC大西洋MHT

图10.8 1958 - 2004年4次Drakkar模拟增加分辨率(2,1,1 /2和1/4°)时，26°N大西洋MOC的月平均变化(以Sv为单位)。所有模拟都由相同的DFS3强制驱动(运行系列G70)。AMOC的值为图10.7所示的1000 m处翻转流函数的值。MERA曲线来自a区域模型北大西洋的1/3°分辨率(Lecointre 2009)

图10.8 1958 - 2004年4次Drakkar模拟增加分辨率(2,1,1 /2和1/4°)时，26°N大西洋MOC的月平均变化(以Sv为单位)。所有模拟都由相同的DFS3强制驱动(运行系列G70)。AMOC的值为图10.7所示的1000 m处翻转流函数的值。MERA曲线来自北大西洋1/3°分辨率的区域模型(Lecointre 2009)。

图10.9比较了2°模式和1/12°模式模拟的时间平均垂直积分(正压)流函数。1/12°模型的解已被平滑并绘制到2°网格上。这两种模式在大尺度环流的位置和平均流的位置上大致一致，但在水平环流中可以看到许多差异，例如北大西洋亚极环流的结构和范围、南大西洋西部的汇流或南极绕极流的锋面结构。显然，分辨率显著提高了模拟的西部边界流、永久锋的位置以及电流速度和传输的振幅的真实感。由于这些改善大多出现在大气区域风暴之发展形成，人们可能会期望使用粗糙和涡流海洋模型的海洋/大气耦合模拟之间发生重大(和潜在的有益)变化。

Penduff等人(2010)对1993-2004年期间观察到的低通滤波和Drakkar模拟了时间依赖的SLA场，以比较大的模型技能

5 93 180 268 355

Drakkar 2°模型

5 93 180 268 355

Drakkar 2°模型

5 93 160 268 355

b Drakkar 1/12°模型

图10.9 (a) 2°分辨率模型0RCA2和(b) 1/12°分辨率模型0RCA12(等高线间距为20 Sv)模拟的平均正压输流函数。为了进行比较，1/12°的解已经用100次的汉宁滤波器平滑，并绘制在2°的网格上

5 93 160 268 355

b Drakkar 1/12°模型

图10.9 (a) 2°分辨率模型0RCA2和(b) 1/12°分辨率模型0RCA12(等高线间距为20 Sv)模拟的平均正压输流函数。为了进行比较，1/12°的解已经用100次Hanning滤波器平滑，并在2°网格尺度年际变化(LSIV)上绘制，即在大于约6°的尺度和大于1.5年的时间尺度上绘制。模型分辨率从2°到1/4°的连续增加显示了LSIV特征的系统改善，特别是更强的年际变化，以及其地理格局的系统改善。这再次表明，中尺度特征的(部分)分辨率比中尺度参数化产生更准确的涡旋通量，不仅涉及平均状态，而且涉及其低频变化。虽然盆地集成量对这种设置中的分辨率变化适度敏感，但当网格尺寸减小时，它们的空间和时间模式(因此它们的潜在动力来源)会得到强烈改善。

10.5结论

在这门课程中，我们使用卫星观测来说明海洋中尺度变率在每个盆地和所有纬度的普遍存在。我们提供了海洋中尺度的动力学定义，基于尺度参数，将中尺度与一般环流联系起来，并提供了运动的特征尺度。我们列出了可能对海洋环流和气候有重要影响的中尺度过程。raybet雷竞技最新在建模方面，提出了两种处理涡流问题的方法。一种是用计算成本高的精细网格来解决涡流(部分到全部)，另一种是在粗糙但计算效率高的网格上参数化涡流。这就提出了已解决/未解决尺度的概念，海洋模式为其所解决的尺度提供了解决方案，这取决于未解决尺度的表示。

我们已经解释过，未解尺度的表示需要一个基于物理基础的“闭合假设”，这在层流模型和涡流模型中是非常不同的。这两种类型的模型都求解相同的方程:相似的数值格式可用于两者。然而，例子表明模型解对数值格式的敏感性取决于分辨率:正如预期的那样，高分辨率模型对用于求解非线性项的数值格式(例如动量平流格式)表现出更大的敏感性。因此，模型发展的方法应该将分辨率的提高与数值格式的改进和子网格尺度的参数化紧密联系起来。

尽管涡流模型和层流模型求解的方程相同，但由于物理和数值原因，它们并不能模拟“相同”的海洋。给出了一个例子，其中粗分辨率解和空间平滑的高分辨率解是不等效的(即参数化仍然不能完全表示未解析的尺度)。分辨率的增加使得中尺度湍流的发展，从而提高了分辨率物理的一致性和模型解的真实性，特别是强流的路径，它们与地形的联系，流速的振幅，以及年际变化的主要特征。然而，一些与气候相关的综合量raybet雷竞技最新，如AMOC和MHT似乎对分辨率相对不太敏感(例如AMOC平均模式及其年际变化)。然而，由于海气相互作用是局部的，这些结果表明，涡流海洋模型应该有助于提高未来气候预测系统的物理一致性。raybet雷竞技最新

为了结束这一过程，我们应该强调(中尺度)涡流分辨率模型仍处于起步阶段。今天的“涡流分辨率”全球模型在赤道的分辨率达到1/12°，但很少有常规使用(大多数网格较粗，即高达约1/4-1/10°)。更一般地说，涡流全球模式对强迫、参数或数值方案的敏感性在很大程度上仍然未知，各种研究小组仍在研究未解决的(亚中尺度)特征的参数化。实际上，涡流全球模型的计算成本和存储需求很大(即使对于目前的超级计算机):未来10年的挑战可能是进行从0(1/4-1/10°)到0(1/12-1/16°)常规气候导向的大规模模拟的转换。raybet雷竞技最新由于计算机的限制，用于10000年古气候追踪的气候模型使用(层流)raybet雷竞技最新海洋成分的分辨率比用于类似ipcc的100年预测的分辨率更粗。反过来，这些耦合海洋模型的分辨率不能像目前在Drakkar-like ocean-only eddy setup中开发的那样好，也不能像目前在区域域上以更高分辨率(例如1/32°或更高)使用的操作模型那样好。一方面，粗分辨率模型不断受益于从高分辨率模型发展而来的参数化。另一方面，这些模式是改进某些涡旋海洋模式组成部分(例如大气强迫)的有效工具，耦合的海洋/大气模式为涡旋海洋模型提供了空气-海洋相互作用的基本反馈。总之，“层流”、“允许涡流”和“消除涡流”海洋模型需要协调开发工作，因为海洋建模人员根据应用需要大量工具。

我们感谢CNRS和CNES对格勒诺布尔ME0M海洋模拟小组的持续支持，以及GENCI (IDRIS和CINES)在超级计算方面提供的非常重要的支持。本课程由GMMC提供支持。Bernard Barnier非常感谢Clothilde Langlais，她准备并教授了与本课程相关的GM90参数化的实际工作，并感谢Tim Pugh，他为实际工作如此有效地设置了计算机设施。我们要感谢Jean Marc Molines, Melanie Juza和Albanne Lecointre他们为课程提供了重要的材料，还有Anne Marie Treguier和Gurvan Madec，他们是我们Drakkar合作的伙伴。

附录

本课程中常用的笛卡尔坐标系(x, y, z)中原始方程的公式。

定义

势温

S盐度p密度u = (u, v, w)速度向量

P压强f科里奥利参数g重力加速度

Dts u v扩散/耗散项

Ft s u v强迫项

(x,y, z)坐标系(东，北，上)

方程

纬向的动力

经向动量

温度盐度d u 1dp

+ (u■V)u - fv =——+ Du + Fu dt po ox dv 1dp

+ (u■V) V + fu =——+ Dv + Fv dt po dy dt

静压近似_ =

速度矢量u = (u, v, w)的无散度

参考文献

Barnier B, Madec G, Penduff T, Molines J-M, Treguier AM, Le Sommer J, Beckmann A, Bias-toch A, Boning C，邓杰，Derval C, Durand E, Gulev S, Remy E, Talandier C, Theetten S, Maltrud M, McClean J, De Cuevas B(2006)部分阶跃和动量平流方案在涡旋允许分辨率下对全球海洋环流模式的影响。海洋动态。doi:10.1007/s10236-006-0082-1 Biastoch A, Boning CW, Lutjerharms JRE(2008)厄古拉斯泄漏动力学影响大西洋翻转环流的年变化。大自然。Brodeau L, Barnier B, Penduff T, Treguier AM, Gulev S(2010)基于ERA40的全球海洋环流模式的大气强迫。查努特J, Barnier B, Large W, Debreu L, Penduff T, Molines JM, Mathiot P(2008)拉布拉多海中尺度涡及其对对流和再对流的贡献。Chelton DB, Schlax MG, Samelson RM, de Szoeke R(2007)大型海洋涡流的全球观测。地球物理Res Lett。德布鲁尔，武兰德C, Blayo E (2008) AGRIF:自适应网格优化的Fortran，计算机地理科学34(1):8-13

Ducet N, Le Traon PY, Reverdin G(2000)来自Topex/Poseidon和ERS-1和-2的全球高分辨率海洋环流测绘。DRAKKAR Group(2007)过去几十年允许涡旋的海洋环流后报。CLIVAR

Eden C, Greatbatch RJ(2008)朝向中尺度涡旋封闭。Fichefet T, Morales Maqueda MA(1997)全球海冰模式对冰热力学和动力学处理的敏感性。朱建忠(2008)高黏滞度、Galerkin截断与湍流瓶颈的关系。物理Rev Lett 101:144501

金特PR, McWillams JC(1990)海洋环流模型中的等旋流混合。海洋物理学报20:150-155

Griffies SM(2004)海洋气候模式基础。raybet雷竞技最新普林斯顿大学出版社，普林斯顿(518+xxxivpages)

格里菲斯SM，阿德克洛夫特AJ(2008)海洋模型方程的制定。In: Hecht MW, Ha-sumi H (eds)海洋建模地球物理专著177。Griffies SM, Gnanadesikan A, Dixon KW, Dunne JP, Gerdes R, Harrison MJ, Rosati A, Russell JL, Samuels BL, Spelman MJ, Winton M, Zhang R(2005)全球气候模拟海洋模式的制定。raybet雷竞技最新杨晓东，杨晓东(2007)质量控制海洋温度和盐度分布的历史和实时数据。J Mar系统。朱anno J, Sheinbaum J, Barnier B, Molines JM, Debreu L, Lemarié F(2008)加勒比海的中尺度变率。第一部分:嵌入式模型和特性的仿真。刘志强，李志强，李志强，等。(2011)基于ARGO采样的混合层性质分布畸变估计。J operoceanogr(提交)大型工作组(1998)海洋行星边界层建模和参数化。在:chassiget EP, Verron J (eds)海洋建模和参数化。Kluwer，荷兰，pp 81-120 Large WG, Yeager SG(2004)海洋和海冰模式的日至年代际全球强迫:数据集和通量气候学。NCAR技术说明:NCAR/TN-460+STR。CGD分部国家大气研究中心大型工作组，耶格尔SG (2008)全球气候学一个年际变化的海气通量数据集。Clim Dyn. doi:10.1007/s00382-008- 0443 -3 Large WG, McWilliams JC, Doney SC(1994)海洋垂直混合:综述和非局部边界层参数化模型。Rev地球物理学32:363-403 Lecointre A (2009) Variabilité océanique interannuelle dans l'océan atlantic Nord:模拟et observabilité。Thèse de l'Université约瑟夫·傅里叶，格勒诺布尔。http://tel.archives-ouvertes．fr /电话号码——00470520 /

Lesieur M(2008)流体湍流，第4版。FMIA 84, R.莫罗系列编。施普林格，多德雷赫特。李志强，李志强，李志强，李志强(2009)在涡流允许分辨率下动量平流方案对电流-地形相互作用的影响。海洋模型29:1-14

Madec G (2008) NEMO，海洋发动机，注释de l'IPSL, Universit_e P. et M. Curie, B102

T15-E5, 4位Jussieu, Paris cedex 5 Madec G, Imbard M(1996)克服北极奇点的全球海洋网格。Clim Dyn 12:381-388

McWilliams JC(2008)海洋涡流的性质和后果。在:赫克特MW, Hasumi H(编)海洋建模在涡流政权，地球物理专著177。美国地球物理联合会，华盛顿，pp 5-15 Müller P(2006)海洋运动方程。剑桥大学出版社，剑桥，291页

彭达夫，刘志刚，刘志刚，刘志刚，刘志刚(2007)1/4°全球海洋数值模拟对海流-地形相互作用的影响。海洋科学3(4):451-535

Penduff T, Juza M, Brodeau L, Smith GC, Barnier B, Molines J-M, Treguier A-M, Madec G(2010)基于年际时间尺度的模式分辨率对海平面变化的影响。Redi MH(1982)坐标旋转的海洋等旋混合。Treguier AM(2006)海洋模型:哪个海洋?见:chassignnet EP, Verron J (Eds)海洋天气预报。赵锐，范志强(2008)基于残差和欧拉模式的中尺度涡参数化及其与允许涡模式的比较。海洋模型23:1-12

继续阅读:GODAE环境下的等纬和混合海洋建模

这篇文章有用吗?

＋1 0