Xa Xb aXX Vyy Xb136
这个估计的方差是
°a = (a-2 + a;2)-1。(13.7)
尽管这个例子很简单,但它显示了高级线性数据同化方法的一些关键特征。首先,请注意式(13.6)中的最优估计
是背景xb和残差y - xb的线性组合。这个词
saxa = a2x(a2x + o2y)-\y - xb) (13.8)
称为分析增量。注意极限ox0(完美背景)和°y ^ 0(完美数据),它们分别产生xa=xb和xa= y。此外,最优的估计方差(13.7)分别小于背景或数据的方差;结合来自背景和观测的信息降低了不确定性。
13.3.2.1例2:向量的估计(最优插值)
将上面的例子推广到向量的估计,假设所有误差都是高斯的,这是习惯的,也是有指导意义的。这就是Gauss-Markov平滑,它构成了许多估计算法的基础。当未知向量表示规则空间网格上的值时,此过程称为最优插值(Bretherton et al. 1976)。这里使用的符号遵循Ide等人(1997)。
假设一个人希望估计一个向量xern,给定背景xb,和一个观测向量y erm。最优插值(也称为客观分析)通常是为了将稀疏观测平滑地插值到规则间隔的空间网格上,在这种情况下,x可能表示网格点上的海面高度值。假设观测向量y = {yi}f=x的每个元素都可以表示为一个线性算子对x(ti)的作用,
h;e RlxN。例如,h.可以在地理经纬度坐标中提取x在空间坐标($p x)处的值。接下来,通过收集测量操作符来定义矩阵he RM xN,使y=Hx。更一般地,观察算子H根据测量的位置和特征(例如,单位)将模型变量x映射到观测向量的等效值。
为了应用贝叶斯定理,必须给出x - xb的概率密度和测量误差s = y - Hx。它们都是均值为零的多元高斯分布;B e RNxN的协方差,即
<(x - xb)(x - xb)T) = B, (13.10)
e的协方差记为r e rmxM。应用式(13.2),我们发现x以y为条件的pdf正比于exp (- 1J(x)),其中
J (x) = (x - xb) TB-1 (x - xb) + (y - Hx) TR-1 (y - Hx), (13.11)
这就是所谓的变分数据同化的目标函数。目标函数,也称为代价函数或惩罚函数,是关于向量x的最小值。
通过一点线性代数,我们可以找到x=xa使J最小的值是xa = xb + K(y - Hxb), (13.12)
其中分析增量为saxa =K(y - Hxb), K的形式为
K = BHr (HBHr + R)-1。(13.13)
分析误差的完整表达式,xa的误差协方差,记为e rNxN
Pa = (B-1 + Hr R-1H)-1。(13.14)
备注:
1.式(13.12)可以导出为最佳线性无偏估计器(BLUE),它使期望误差(eTK(xa - x))2最小化,其中ek e Rw是指向k方向的基向量。类似地,估计器也使期望均方误差Tr((xa - x)(xa - x)T)/N最小化。当模型动力学和测量算子是线性时,这些事实是BLUE、变分-和基于卡尔曼滤波的状态估计等价的基础。
2.当在实践中使用最优插值时,上面的公式经常被简化,以便在每个网格点上的分析仅从附近影响半径内的数据计算Lorenc (1986);戴利(1991)。
3.上面写的J(x)也称为惩罚函数或代价函数。分析场xa是它的最小值。当误差为高斯分布时,1J为负对数似然函数。
4.因为H是线性的,所以J是凸的并且具有唯一的最小值。当H表示非线性算子时,可能存在多个最小值。
5.可以在目标函数中添加额外的约束,例如抑制某些动态。这可能使求解过程相当复杂,并可能掩盖B或R在正确解释背景和测量误差的协方差结构方面的失败。
6.目标函数的条件数是指J的二阶导数的Hessian矩阵的最大与最小特征值之比。Hessian的特征值谱可以解释为J等面的主轴轴的曲率。
7.当高斯误差假设正确时,Hessian矩阵H = d2 J/dx2与分析误差协方差Pa之间的关系为Pa = 1H-1。
8.上述形式可以应用于连续场,而不是RN中的向量。在这种情况下,x通常是一个向量函数而J则是一个惩罚函数。最小V J = 0的平稳性条件必须用变分法推导出来;结果就是欧拉-拉格朗日方程。它与平滑样条理论密切相关,B-1是一个正定对称微分算子(Wahba 1990)。
2044 60 80 100 20 40 60 80 100
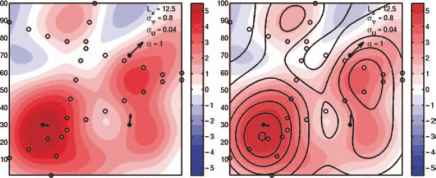
图13.4例2:最优插值。左图显示了海面高度^(x, y),由理想卫星地面轨道上的n观测(用彩色表示测量值的黑色开放圆圈)和对表面流(用箭头填满黑点)。右边面板显示插值场(黑色轮廓)覆盖在真实海面高度。右上角的参数在文本中定义。从中可以看出大流量的特点,如大流量anti-cyclonic涡流,在插值场中被重构
2044 60 80 100 20 40 60 80 100
图13.4例2:最优插值。左图显示了海面高度^(x, y),由理想卫星地面轨道上的n观测值(用颜色表示测量值的黑色开放圆圈)和对海面洋流的三次观测值(用箭头填充的黑点)估计。右边面板显示插值场(黑色轮廓)覆盖在真实海面高度。右上角的参数在文本中定义。从中可以看出大流量的特点,如大流量anti-cyclonic涡流,在插值场中被重构
9.当模型分辨率增加到连续极限时,用连续场来解释对于正确理解目标函数的条件作用至关重要(Bennett和Budgell 1987;班尼特1992年)。线性代数的语言不适用于分析增量的空间规律性(可微性)。
最优插补示例如图13.4所示。要估计的向量x是在一个100km × 100km的方框中一个常规的1km网格上的海面高度。用^(x, y)表示海面高度场,网格上x的元素为^(xj, yj)。在这个理想的设置中,有30个海平面高度的观测数据
对于I = 1,…沿着三条卫星地面轨道(彩色圆点)。假定电流是进来的地转平衡与表面压力梯度,近表面电流有3个观测值(带箭头的黑点)。u分量由
继续阅读:伴随数据同化方法
这篇文章有用吗?