地球

最后一次更新在星期四,09年2月2023年|无线电掩星

图1示意图的掩星几何学。讨论的各种数量的主要文本nr罪英尺= p =常数

f是射线方向之间的角度和半径矢量r(图1)和n是吗折射率。由于GPS和LEO卫星大气以外,n = 1(这里我们忽视电离层),由此可见,p = rG罪fG = rL罪fL,等于射线之间的水平距离和地球的曲率中心。

当考虑大气水平梯度,形势的变化。复杂波场的非均匀介质可以被写成以下形式:u (x) = (x) exp(反向(x)),其中x = (x ')是坐标向量,k = 2 n / x是波数,x是波长、振幅(x),和& (x)是程函。不均匀的几何光学媒体是基于程函方程(Kravtsov和奥洛夫1990):

射线是汉密尔顿所描述的系统,哈密顿函数遵循从情商。(2):H (p (x) = 1/2■(p2 - n2 (x)),其中p = v是动力。相关的汉密尔顿方程一线采取以下形式:

dx dp

2 d6 de pe = r - f = nr - = nr罪;

从我们看到的第一个方程在极坐标的角组件动量等于射线影响参数,因为它被定义为球对称介质,即。,p =体育。第二个方程推广斯涅尔定律(Eq。1),表明p是唯一不变的球对称介质(dn / = 0)。当讨论大气的RO测深与水平梯度影响我们必须考虑两个参数:pG = rG罪fG和pL = rL罪恶fL。它们之间的关系遵循从情商。(4):

在处理无线电掩星数据不能直接确定两个影响参数,在接收机和发射机。相反,可以找到一个有效的影响参数。从计算,光路的时间导数&沿着里奥(t)测量观察t轨迹作为时间的函数,使用相同的公式的独特影响参数在球对称的气氛中。的一般表达式如下:

= rG cos G + rGOG罪f G + rL因为L - rLOL罪f L (6)

■rG - PG ^ = - V rL - PL L + Pg6g - PL°

这里,在最后表达我们忽视水平梯度垂直于掩星飞机。为有效影响参数P有隐式定义如下:

一个= pe + - p2 + rL - p2。(7)

光路的使用以下公式:

是过度的阶段,我们可以获得参数的有效影响轨道数值和相位多余的数据解决Eq。(7)在单一雷地区,或通过应用正则变换(CT) (Gorbunov 2002;Gorbunov和劳里岑2004),全光谱反演(FSI)(詹森et al . 2003年),或相匹配(詹森et al . 2004年)展开多路径传播的方法。这些技术都是基于假设的有效影响参数所定义的Eq。(7)是一个独特的射线歧管的坐标,换句话说,不同的光线有不同的p。pG(隐性)关系、pL和p是由方程式。(5)、(6)和(7)。它包括水平梯度折射率dn /做。

在强劲的水平梯度随高度变化的有效影响参数可能不再代表一个独特的射线歧管的协调。处理这种情况的一个可能的方法是修改CT方法,射线歧管预计坐标不同p。就其本身而言,这可能是直接的,除了这个新的独特的坐标是未知的,因为它取决于未知的水平梯度折射率。这里我们将跟随另一个前景:而不是修改CT方法,我们将估计弯曲角错误由于强大的水平梯度。

3广播全息误差估计

波信号的无线电全息分析可以在t -和p-domains执行。收音机全息(或滑动谱)分析t域广泛用于视觉RO数据的分析以确定反射光线,等。不同类型的问题(Igarashi et al . 2000;Gorbunov et al . 2005年)。收音机全息分析p-domain允许误差估计的弯曲角度检索(Gorbunov et al . 2005年)。

这里我们将弯曲角误差的估计方法由于尚未充分展开多路径结构(图2)。

在CT方法中,波场u (t)映射到参数表示傅里叶积分算子的影响(FIO) &。在转换后的空间,u (p) = (p) exp(反向的(p))可以进行滑动光谱分析(Gorbunov et al . 2005年):

p-Ap据美联社exp (W / 2 (p ^

美联社窗口宽度,& (p)的模型相变异p-domain, %是弯曲角的变化。m (p, %)附近的一个最大的真实弯曲角% = e (p) - e (p),其中e (p)是弯曲角对应的平滑模型和(p)。

我们使用美联社= 250 & (p)和模型计算&”(p)平滑窗口美联社。然后弯曲角误差估计的谱宽度(参见示意图宽度表示在图2)的两个左面板(Gorbunov et al . 2005年):

如果H p %) i2 % 2 d % y / 2 Se (p) = n L2J•(10)

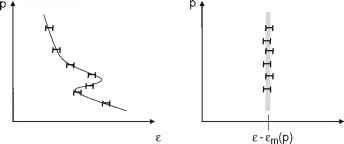
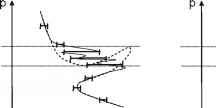
图2无线电全息的原理(滑动频谱)弯曲角的估计错误。:这种情况的参数是一个独特的协调和影响光谱窄;底:情况水平梯度导致p没有独特的坐标线管汇。光谱宽度允许弯曲角的估计错误

非唯一雷地区滑动频谱将展示一个广泛的结构,最终映射到一个更大的弯曲角误差比的情况下只有一个射线对于一个给定的现值的影响参数。

4数值模拟

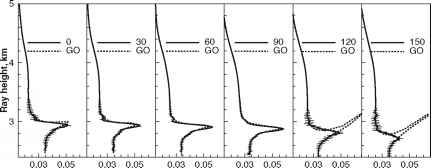
为数值模拟我们选择一个人工掩星的例子,那里的情况的非唯一投影射线歧管参数轴发生的影响。模拟掩星是基于一个ECMWF有关字段从2月5日,1997年,UTC 00:00。我们模拟水深点同一地区的不同的方位角》。另具有掩星平面之间的夹角和地方北方向。我们改变了方位,从0°- 330°和30°的一步。结果12几何光学配置文件(模拟“真相”)是图3所示。这些资料是通过几何光学射线跟踪。这里弯曲角e所示作为射线影响高度的函数定义为p - rE,再保险是地球的曲率半径。最强的的影响

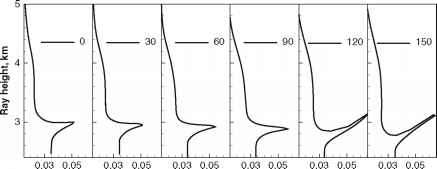
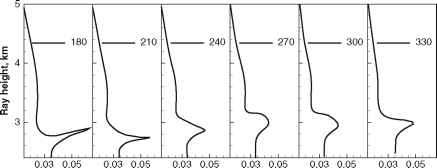
图3真实模拟弯曲角的测深资料相同的位置12.4°N, 170.9°W不同方位角》(从0°- 330°,30°)的步骤。另具有掩星平面之间的夹角和地方北方向。建模是基于ECMWF字段2月5日,1997年,UTC 00:00

多值弯曲角剖面是方位角观测到120°、150°、180°。非唯一的一个小区域雷流形投影的方位也可以注意到0°。

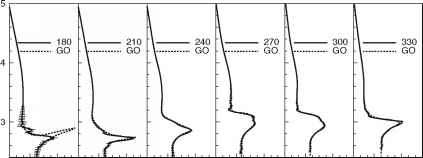
图4展示了CT-retrieved弯曲角配置文件。这些概要文件从人工RO波动光学模拟的数据检索(Gorbunov 2002)。因为标准的CT技术依赖于参数p的影响作为一个独特的射线流形坐标,它是无法复制真实的多值方位角120°弯曲角的概要文件,150°和180°。

小面积多值弯曲角剖面的方位也可以注意到0°。单值配置文件检索。另,独特性的假设射线多方面的参数化的影响参数p是破碎的,明显的增加了基于情商水平的估计错误。(10)。在图5中展示p-domain运行的无线电全息谱。三个案例可以看出,光谱宽度增加地区的多值投影射线歧管,符合理论预期。然而,误差小于之间的差异

0.03 0.05 0.03 0.05 0.03 0.05 0.03 0.05 0.03 0.05 0.03 0.05

图4真实模拟弯曲角的概要文件(去,虚线),检索模拟弯曲角的概要文件(实线)和他们的错误估计测深在同一位置12.4°N, 170.9°W不同方位角》(从0°- 330°,30°)的步骤。另具有掩星平面之间的夹角和地方北方向。建模是基于ECMWF字段2月5日,1997年,UTC 00:00

0.03 0.05 0.03 0.05 0.03 0.05 0.03 0.05 0.03 0.05 0.03 0.05

120 1 180

-0.004 0 0.004 0.004 - -0.004 0.004 - -0.004 0

英航偏差,rad英航偏差,rad英航偏差,rad

图5滑动光谱在p-domain三掩星平面方向,弯曲角是一个多值函数的影响参数(上面的文本数据对应方位值)。一个观察光谱的展宽值多路地区约2.75 -3.25公里(图3)。

-0.004 0 0.004 0.004 - -0.004 0.004 - -0.004 0

英航偏差,rad英航偏差,rad英航偏差,rad

真正的多值和CT-retrieved弯曲角。这是因为弯曲角的飙升包含一小部分的能量,这是分布在拉伸片段的射线歧管。

5的结论

CT / FSI方法使用这一事实的影响参数p是独特的光线空间的坐标。这种情况是普遍有效的球对称的气氛。在大气水平梯度折射率这并非总是如此。强大的水平梯度导致沿射线的影响参数的变化而不是不变的。这就是为什么一般不可能引入的概念影响大气参数与水平梯度。相反,我们引入了所谓的有效影响参数使用相同的定义从多普勒频率为球对称的气氛中独特的影响参数。在强劲的水平梯度随高度变化,有效影响参数的扰动可能会导致的非唯一投影射线歧管轴的影响参数。在这种情况下,弯曲角可以有效影响的多值函数参数。因为CT / FSI方法依赖参数的影响被沿着射线歧管独特的协调,因此,在这种情况下,该方法将无法正确获取弯曲角概要文件。

在普通CT形式它可能会引入一个新的坐标,除了影响参数,这样光线歧管应该有一个独特的投影到相应的轴。不过,这个新坐标的定义取决于特定的大气领域,因此,它不能被指定的先验。另一个机会的估计是错误的弯曲角度通过无线电全息检索p-domain(滑动谱)分析。数值模拟与实际大气领域从re-analyses ECMWF表明,误差估计增长强劲水平梯度的存在导致多值几何光学弯曲角的概要文件。这使得标准CT / FSI技术辅以广播全息误差估计一个有价值的工具,用于分析RO数据在所有情况下。

引用

Gorbunov我(2002)规范变换方法处理无线电掩星数据在对流层较低。无线电Sci 37 (5), doi: 10.1029/2000 rs002592 Gorbunov我,劳里岑KB(2004)分析波域傅里叶积分算子及其申请无线电掩星。无线电Sci 39 (4), doi: 10.1029/2003 rs002971 Gorbunov我,劳里岑KB, Rhodin, Tomassini M, Kornblueh L(2005)冠军radio-occultation测深实验数据的分析地球大气层。Izv大气压海洋phy 41 (6): 726 - 740

Gorbunov我,劳里岑KB, Rhodin Tomassini M, Kornblueh L(2006)无线电全息过滤、误差估计质量控制无线电掩星数据。111 J“Res (D10雷竞技csgo105), doi: 10.1029/2005 jd006427 Igarashi K, Pavelyev, Hocke K, Pavelyev D, Kucherjavenkov IA, Matyugov年代,Zakharov,雅科夫列夫O(2000)无线电全息原理观察大气中自然过程和检索气象参数从无线电掩星数据。地球行星空间52 (11):893 - 899

詹森,罗曼女士,Benzon HH,尼尔森(2003)全谱反演的无线电掩星信号。38岁的电台Sci doi: 10.1029/2002 rs002763詹森,罗曼女士,尼尔森,Benzon HH(2004)无线电掩星信号的几何光学相匹配。无线电Sci 39 (3), doi: 10.1029/2003 rs002899 Kravtsov是的,奥洛夫易(1990)几何光学不均匀的媒体。斯普林格出版社,

柏林,海德堡,纽约罗曼女士(2006)动态误差估计无线电掩星弯曲角度检索的全谱反演技术。无线电Sci 41 (RS5005), doi: 10.1029/2005 rs003396 Sokolovskiy SV,出身地C, Lenschow DH,郭YH,尖刺外壳RA,妇女不同WS,亨特直流(2007)观察湿对流层与无线电掩星信号来自宇宙。“Res列托人34 (L18802) gl030458 doi: 10.1029/2007

相位变换算法进行无线电掩星数据处理

抽象描述的相位变换算法和派生的肝仪器数据处理。该算法允许将无线电掩星中立的弯曲角度恢复当地球对称大气中多路径的存在。仪器操作和载波相位重建被描述为开环模式和闭环模式。

1介绍

全球导航卫星系统(GNSS)无线电掩星接收机大气探测(肝)仪器(Luntama 2006;威尔逊和Luntama 2007)的仪器由ESA / EUMETSAT METOP卫星(METOP-A、METOP-B和METOP-C)。肝的数据,结合其他数据,用于估计大气温度、压力和湿度资料(数值天气预报)以及研究电离层总电子含量(TEC)。一个先进的处理算法估算中性弯曲角度从肝数据描述和讨论;这个算法是相位变换算法。

2肝仪表和信号再生

肝仪器包括三个天线(GVA,河,GZA),三个射频调节单元(RFCUs),一个肝电子单元(GEU)和利用项目(Loiselet et al . 2000年)。每个天线连接到其RFCU和每个RFCU GEU连接。GVA和河视图地球的卫星速度方向的肢体和卫星anti-velocity方向,分别。

EUMETSAT Postfach 10 05年55岁,64205达姆施塔特,德国的电子邮件:(电子邮件保护)

施泰纳et al。(eds),新视野号在掩星的研究中,

DOI 10.1007 / 978 - 3 - 642 - 00321 - 9.3,©斯普林格出版社柏林海德堡2009年版

这两个天线有18双频率接收数组元素在一个3×6。GZA是宽波束、低增益天线上面查看的区域卫星;这个天线有两个接收元素为每个频率。肝接收器有16个复杂通道分配给GZA天线,4复杂通道分配给GVA天线,和4复杂通道分配给河天线。因此,接收机可以追踪到8 GPS卫星(L1和L2)与GZA天线用于导航,同时观察2掩星GVA天线(L1和L2)和2掩星河天线(L1和L2)。每个通道可以分配给一个频率和卫星。

在天线接收到的信号是受射频滤波、低噪声放大、转换从射频到如果在RFCU有关。然后传送到GEU数字化、过滤、受到进一步的数字转换,de-spread,最后进行代码和载波相位跟踪。GEU中的最重要的元素是A / D转换器,阀瓣asic AGGA-2A asic,数字信号处理器(DSP)、频率发生器(FG),和超级稳定的振荡器(USO)。如果从RFCUs信号数字化的A / D转换器和数字过滤盘asic和向下转换。AGGA-2A asic执行所需的相关性和积累操作DSP的控制之下。接收者的措施,在合适的条件下,可观测参数为每个GPS卫星跟踪如下:(1)L1 C /代码阶段,(2)L1 - code阶段,(3)L1载波相位,(4)L1信号振幅,(5)L2 - code阶段,L2载波相位(6),(7)L2信号振幅。这些测量是印有肝仪器测量时间(IMT)。载波跟踪阶段使用跟踪循环给一个非常狭窄的频段输出(50赫兹)除了可怜的相位噪声条件下带到基带载波相位的使用跟踪法,基于预期行为,这将导致更广泛的带宽输出(1000赫兹)。

肝仪器执行导航、卫星预测和选择、获取和跟踪和数据处理。导航需要计算METOP从获得的数据的位置和速度GZA天线。卫星预测和选择需要确定哪些GPS卫星跟踪,当这是完成导航和掩星。卫星获取包括载波频率同步和代码生成器的接收机接收到的信号传播。C /收购一个代码是基于一个二维搜索范围定义的代码阶段和载波频率使用最大似然决策标准;搜索简化的如果是一个好的导航解决方案是可用的。当C /代码阶段被确定了C /代码跟踪和L1频率跟踪循环开始。代码跟踪利用归一化积鉴别器操作在同相正交组件的早期、晚期,守时相关器的输出AGGA-2A ASIC估计代码抵消。频率跟踪是用二阶环路滤波器补偿使用代码。开始前L1载波相位跟踪回路采用基于FFT的频率估计的频率误差减少到可以接受的水平。 The carrier phase tracking is performed with an arctangent phase discriminator and a third order Costas loop. When L1 carrier tracking has been achieved the P-code on the L1 carrier and the L2 carrier can be searched; the search makes use of the hand over word from the navigation data from the tracked C/A-code. If the P-code is encrypted a code-less acquisition and tracking scheme must be used employing cross-correlation of the P-codes on the L1 and L2 channels. When the P-code on the L2 carrier is tracked, L2 carrier phase tracking can be started.

的第一部分肝数据处理地面接收到的载波相位重建涉及天线相位中心在一个给定的通道(通道)从数据产生的乐器。这涉及到增加的信号转换被固定下来,跟踪循环或法治最终转换。这个重建是相当复杂和仪器特定的流程。产生的信号称为再生信号。

让一组N再生阶段样品和相应的肝IMT对于一个给定的通道和一个特定的掩星是:

这些IMT *是*印在ADC。再生阶段是由以下方程:

2 n fGps (n)

r („ECI (REF \ ECI / / REF \ \

GGREL-TOF VrGRAS-ANT (m) VRX j”以序列(n)蚂蚁发行)

+ 2 nfgps (n) (Aimt (iRXF)——agp (n)(我'Txf))

+ ^ ch(我)(0 (irxef), H4XP) Tk (irxef))

+ ^常数

在情商。(2)再生阶段有以下条款的意义。第一和第二项与几何发射机和接收机之间的延迟;第一项是正常的几何距离,第二项是广义相对论的修正由于地球引力场的影响。第三项与发射机和接收机的时钟偏移对惯性参考时间,iREF。第四和第五条款与对流层和电离层,相关联的阶段,它需要恢复。第六项是乐器特征项。第七项是循环滑项;这一项是理想的零但是周期会发生如果发生相变速度超过在掩星接收机可以跟踪。第八,上学期是一个常数相抵消。

测量对流层的最低部分困难是由于低信噪比(信噪比)的GPS信号和强烈的大气调制。接收器有问题在维护阶段锁定GPS载波相位设置掩星,在获取锁相掩星。肝接收机输入一个“原始采样”(RS)测量模式(也称为开环模式)的跟踪L1 C /代码是可能的,但在载波相位锁相是不可用的。在原始采样模式下肝测量数据包含相关器的输出单位接收采样1000 Hz。

肝接收器使锁相跟踪模式之间的切换和RS自动模式。在设置掩星肝接收机通常为一个频率跟踪模式转换跟踪L1代码阶段,载波相位和振幅时的锁相L2信号丢失。在某种程度上,当射线路径切线高度低对流层,接收方也可能失去L1载体上的锁相。接收机软件预测通过监测L1信号进入RS模式如果L1锁相的不稳定超过预定的水平。这样可以确保观测数据的连续性。这个设置掩星将结束时的测量上的锁L1编码阶段。

上升的掩星是稍微复杂的测量作为接收机跟踪,直到没有背后的GPS信号可用从地球的肢体。上涨的开始时间掩星接收机预测的车载软件基于GPS和传播METOP轨道。GPS轨道计算通过使用GPS导航信息和METOP轨道是由车载导航解决方案。正常肝接收器应该能够很快获得L1 C /代码阶段后的信号。此时锁相的L1航母是不可能和测量上升的掩星从肝接收器在RS模式开始。崛起的掩星的RS模式将继续,直到接收方已经获得了一个稳定的L1载波相位锁相。当L1载波相位锁定已经实现,接收机输入单频跟踪模式。最终L2代码阶段信号将会变得强大到足以被跟踪的接收器。稳定后得到了L2载波相位锁定,接收者将进入两个频率跟踪模式。

在RS模式最终转换是通过使用法律的参数作为输出数据的一部分。这使得载波相位重建在地面处理。

之间的差异主要有两种载波相位测量中提供RS模式和跟踪环路锁定时提供。在原始采样模式下采样率为1000 Hz和导航信号消息(销售经理)不是抽样数据的解调。这个销售经理在原始采样信号是一个二进制信号调制模式载波相位在50 Hz。0到1或者1 - 0过渡发生载波相位转移由n弧度。在地面处理的原始采样数据结合闭环数据模式。原始采样模式下数据必须同意闭环数据重叠区域的开始。让这发生的所有原始采样模式数据由0或n旋转弧度。最后一部分(或第一部分的崛起的掩星)单一频率的跟踪数据是不可靠的,因为失去了锁相接收机。因此,重叠的闭环数据就会被丢弃。

有两种方法可以把销售经理从原始采样模式数据:销售经理的销售经理是自动删除或移除使用知识,从另一个来源是什么。自动销售经理移除基于可能性定位的一个销售经理n跳跃在该地区附近的原始采样模式数据到闭环数据。一旦一个载波相位的位置增加n是发现所有其他潜在的位置确定的转换。原始采样模式因此载波相位可能平均值的地区(例如,20样品)的销售经理是常数减少噪音。以这种方式销售经理可以估计和删除从原始采样模式载波相位旋转的阶段0或n的值根据样本的销售经理。自动删除将变得更加困难进一步消失从闭环数据时,将失败与大气相关联的相位噪声方法与销售经理相关的n跳跃转换。原始采样模式数据的经理不能删除必须丢弃。基于知识的消除使用一个经理位流记录由一个独立的GPS接收器(例如,网络地面接收器)。完整的销售经理然后玫卫星相关的序列与接收到的RS数据和相匹配的跳跃经理转换移除。基于知识比自动删除方案更可靠,但需要销售经理序列的连续记录所有的GPS卫星。

3相位变换算法

经典几何光学算法适用于没有提供多路径传播发生在大气中。如果多路径传播发生时,需要一个更复杂的算法来恢复中性弯曲角的函数的影响参数,即相位变换算法。相位变换算法最初是由a . s . Jensen派生(詹森et al。2003、2004、2006),在一个稍微不同的形式。推导了这是明确的。

执行阶段变换算法再生阶段必须首先纠正(a)仪器特点,广义相对论(b)和(c)时钟漂移。这些修正后与单位执行一个复杂的信号振幅是由产生的再生阶段^ REG-B使用以下方程:

RrEG-B (tRMt) = exp (+ i ^ reg-B(泰爱泰党))(3)

下一个执行阶段变换:

u (p) =«(rRMT) ^ REG-B(4吨)exp(我ß(p, tRMT)) drRMT,(4)乔m是一个权重函数介绍了防止振铃和¡3 (p、t)是参考相位函数参数p。弯曲角的影响是由以下方程:

L1和L2的弯曲角度频率可以平滑,然后结合中性弯曲角。

一个(p) =«李(p) + 2 _L2 2(«李(p)——«L2 (p))。(6)

参考相位函数是由以下方程的几何被称为相位变换的时间积分(IMT时间或引用)。

ß(P T) = + T I V rLEc以序列(T) - P2 + V (T) - P2 +公关(T)

- p反正切

Vrleo (t) - p p vrgps (t) - p2 %

f rLEO (T)■以序列(T)。

相位变换算法本质上是一个匹配滤波器的选择肝接收器收到的信号部分的信号与一个特定的相关影响参数。相位变换算法从而允许弯曲角恢复的多路径提供大气(本地)球对称。

4相位变换算法的推导

相位变换算法是最好的理解通过回顾它的推导过程;这是下面。考虑图1(生于1983年,狼)。

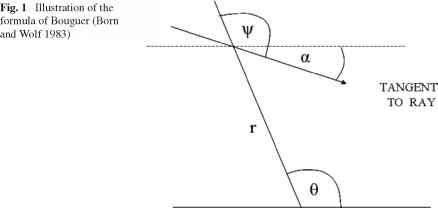
从图1看出:

ds = r余割(^)d < 9 = V (dr) 2 + r2 (d < 9) 2。(9)

为球对称大气布格的公式,Eq。(10),有效p = n (r) r罪(^)。(10)

因此

^ =±p。(2)博士r * Jn2 (r) r2 - p2

从GPS卫星的相位沿射线路径的肝METOP卫星接收机是由:

p = - J n (s) ds = - J n (r)博士J 1 + r 2 (-) (12)

因此

2 n n2(星期五r)”2 n fr2 n2 (r)”

^ Jro yn2 (r) r2 - p2 ^ Jr0 y n2 (r) r2 - p2

以上r0最接近的程度。现在考虑这些积分之一:

X Jr0 tJn2 (r) r2 - p2

使用单位:

1 dn

1 dn n2r =——(n2r2)——(n2r2 - p2)——p2

2 n n博士和博士方程:

积分就变成:

推荐- - - - - -我Vn2 (r) r2 - p2d (ln (n))博士

X Jro jn2 (r) r2 - p2从图1博士和布格公式的发现:

Vn2博士(r) r2 - p2 n ^ n2 (r) r2 - p2 1 r d6 _ p

= * n2 (r) r2 - p2博士r '

因此

m = - t”Vn2风湿性关节炎(rA) - p2 + aA0

n2 (r) r2 - p2,是。

因此的阶段

狮子座- P2 + V以序列- P2 + Pa

2 r ynw-pdilnnu

,参照图2:

——反正切

现在考虑积分:

rTiMr u (p) =„(zRXT) ^ reg-b (r r | T) exp (ifi (p, tRMT)) d tRMT乔

* REG-B (tRMT) = AreG-B (tRMT) exp (+ ip (p, tRM))。

因此

/»Timt u (p) -«(tRXt) Areg-b tRXt exp(我< p (p, tRMt)——ß(p, tRXt)) d tRMt乔

积分可以评估(大约)固定相的方法是:

^«(rRXT0 Areg-b (tRXt0 exp (iv (p -我ß(p, tRXTi))

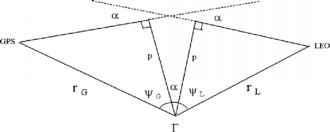
: 图2说明了掩星平面几何

在哪里

P (P t RXT1 > - P (P t RXTx) = arg (u (P))。(30)

现在P (P、t)可以任意选择;如果P (P、t)选择的是:

P (P、t) = t (^ eo (t) - p2 + 7以序列(t) - p2 + P (P t ^ j (31)

在哪里

vrGps (T) - P2 \ (J7 ^ eo (T) - P2

然后参照Eq。(24):

p, n) -ß(p, n) = - x / V«2 (r) r2 - p2 7博士。(33)

因此,我们有:

d, x ^ 4 n d f ~ 2 d (ln (n (r)))

——(p (p, T1) - p (p, T1)) = - - - Vn2 (r) r2 - p2是

X Jro V«博士2 (r) r2 - p2 4 n (2)

一个2 n

方程(34)建立了期望的结果。推导过程的主要步骤是:(i)表达发射机和接收机之间的修正阶段给出Eq。(24),(2)解决Eq。(28) u (p)的固定相的方法,(3)注意到如果p (p t)选择是由(31),那么情商Eq。(33)将arg (u (p))和(iv)观察参数的导数(u (p))对p弯曲角成正比从情商。(34)。从推导,对弯曲角的所有信息都包含在(纠正)再生肝接收机相位测量。不使用信号的振幅。

相位变换算法是有效的对任何航天器轨道提供了一个掩星飞机存在(至少近似)。它是一种精确算法和不是一个近似。全谱反演(FSI)算法(詹森et al . 2003年)是一个近似相位变换算法的适用假设地球和圆球形飞船轨道在同一平面上。在这种情况下Eq。(4)可以用傅里叶变换近似。

引用

生米,狼E(1983)光学原理,第六版。英国剑桥大学出版社,詹森,罗曼女士,Benzon HH,尼尔森(2003)全谱反演的无线电掩星信号。无线电科学38 (3),doi: 10.1029/2002 rs002763詹森,罗曼女士,尼尔森,Benzon HH(2004)无线电掩星信号的几何光学相匹配。无线电科学39 (RS3009) doi: 10.1029/2003 rs002899詹森,Benzon HH,罗曼女士,尼尔森(2006)处理无线电掩星数据的全谱反演技术:概述和最近的进展。:Foelsche U, Kirchengast G,施泰纳AK (eds)大气和气候:掩星的研究方法,斯普林格出版社,德国海raybet雷竞技最新德堡纽约,95 - 112页Loiselet M,前锋N, Menard Y, Luntama LP(2000)肝- Metop以gps大气

测深仪。ESA公报102,pp 38-44 Luntama JP(2006)操作EPS肝测量系统。:Foelsche U, Kirchengast G,施泰纳AK (eds)大气和气候:掩星的研究方法,施普林格,柏林海德堡,raybet雷竞技最新页147 - 156,doi: 10.1007 / 3-540-34121-8威尔逊瞬,Luntama JP(2007)先进的肝仪器数据处理算法。:地球科学和遥感研讨会,2007年雪茄烟,IEEE国际,巴塞罗那,西班牙,页1049 - 1054,doi: 10.1109 / IGARSS.2007.4422981

利用机载GNSS接收器检测大气湍流

第2 Cornman, a·威克利上面古德里奇,r . Frehlich

抽象方法估算湍流强度从GNSS-aircraft掩星。的理论基础是标准的弱散射理论随机电磁波传播的媒体。修改这些技术来处理一个发射器和接收器之间相对运动。模拟方法被用来评估强度的敏感性两个未知参数估计湍流长度规模和动荡的接收机的距离。结果表明,估计是高度敏感的后者和前者相对不太敏感。提出了迭代技术,使用估计的距离参数来提高强度的评估。结果表明,考虑到这个问题,假设迭代技术提供相对准确的估计湍流强度参数。

1介绍

有一个漫长而卓越的历史研究的电磁(EM)通过随机波传播媒体(cf。Tatarskii 1971;Yeh和刘1982;Ishimaru 1997)。这些作品提供了一个坚实的理论基础为估计的统计性质中性大气和电离层通过接收到的电磁信号的统计特性。大气湍流的特点,可以推导出,例如,相关性和/或光谱分析的相位和/或接收信号的振幅。过去,大量的实验分析在这一领域进行了地面发射器和接收器(例如,雷达和激光雷达),以及地面接收器和太空发射器。随着全球导航卫星系统(GNSS)星座,可用的新途径已成为研究地球大气的湍流特性。部署越来越多的低地球轨道(LEO)卫星高质量、高采样率receivers-provides湍流测量的非常有价值的新来源:

博尔德市国家大气研究中心美国电子邮件:(电子邮件保护)

施泰纳et al。(eds),新视野号在掩星的研究中,

GNSS-LEO掩星。有许多其他实际应用可以受益通过湍流测量(和合成气候学)GNSS-aircraft掩星。例如:空间天气(朝圣et al . 1994), trans-ionospheric通信链路(Secan et al . 1997),航空安全与导航系统(七叶树果实et al . 2003;Cornman et al . 2004),地面GNSS接收器的准确性(Ganguly et al . 2004年),以及在测量大气湍流状态变量的影响从GNSS-LEO掩星(Kursinski et al . 1997;Gorbunov和Kirchengast 2005)。

下面介绍的方法和结果从一个更全面的报告准备的波音公司。

2 Theory-Weak散射

波传播的基本理论问题通过一个随机的媒体中描述各种各样的引用,例如,Tatarskii(1971)或石丸(1997)。特定的应用程序来测量电离层此前直接从基本理论也被开发(cf。叶和刘1982;Bhattacharyya et al . 1992年)。进一步应用这个理论GNSS-LEO主席Vorob中讨论的问题是,菅直人(1999)和Cornman et al。(2004)。在下面,后者引用作为起点。

由于发射机和接收机正相对,坐标系统的起源的问题是被接收器。在这种情况下,位移矢量p平面上垂直于视线(LOS)发射机和接收机之间的一阶p = Veffr,其中t是时间的变化而发生位移。假设湍流各向同性在垂直的平面上,它只能位移矢量的长度的函数,| | p | | = | | Veff | | t,哪里| | Veff | |不移动的气氛和球面波传播的

HVeffWII =

其中n是在洛杉矶的距离从发射机(n = 0)到接收器(n = R)。VT是发射机的速度,虚拟现实是接收机的速度,同时计算完整的三维向量上的投影到平面横向到洛杉矶。它可以表明球面波的频谱测量平面上垂直于洛杉矶,对数幅度波动的折射率,x,是由镍+ / 2

l | Veff (n)会

dn,它假定动荡驻留在一片集中在n1和长度在洛杉矶;k是传输信号的波数;再保险是指真正的一部分;C2是湍流强度(也称为结构常数);U是第二类的合流超几何函数,和r是伽马函数(阿布拉莫维茨和Stegum 1972);x = 2 nf / | | Veff | |;y = x2 + l2;L0湍流积分长度的规模;一个= n (R - n) / kR;和一个= 0.033。 A von Karman model for the isotropic index of refraction spectrum is used in Eq. (2) (Ishimaru 1997). Note that the Kolmogorov case is obtained by setting L0 ^ to. The Kolmogorov model is a power law at all wavenumbers. It is valid in the so-called inertial subrange of wavenumbers—far away from both the energy-producing scales (small wavenumbers) and the dissipation scales (large wavenum-bers, Tatarskii (1971)). So, theoretically it cannot be a valid model at the smallest wavenumbers (it goes to infinity). In this subrange, the index of refraction spectrum is only a function of the single intensity parameter, C2. The von Karman model has the same large wavenumber limit as the Kolmogorov model (power-law), but at small wavenumbers, it asymptotes to a constant (a function of both C;2 and L0), which ensures finite energy. The plane wave propagation case is given by setting a = (R — n)/k. For turbulence in the ionosphere, a different set of coefficients are required as well as changing the k2 factor to k—2, but the rest of the formulation is the same. If it is further assumed that the length of the turbulence patch An is small enough such that a mid-point approximation to the integral in Eq. (2) is an accurate one (given some criteria), then

(= ^ k2ACfruAn 4/3。j 2 / 3) _ ^ x VefKm) \ sr (5/6)

应该注意的是,通常不会足够小,这样一个中点逼近是准确的;因此,补丁必须分解成许多小段,在每一个近似是可以接受的。关于这个主题的详细讨论超出了本文的范围(注释在教派。4)。然而,为了简化问题,结果下面的假设中点逼近是不够准确的。

3的结果

3.1对数幅度谱:解析形式

接下来,考虑情商的敏感性。(3)对未知参数,L0和n1。其他未知,合并后的参数C ^ (n1)只会改变曲线的整体水平。图1显示了对数幅度谱L0保持固定时,R - n1(在洛杉矶的距离从飞机到湍流补丁),是多种多样的。参数值:10 = 3.0公里和R - n1 ={10、50、100、200}公里。注意,在下面的分析,假设之间的角度

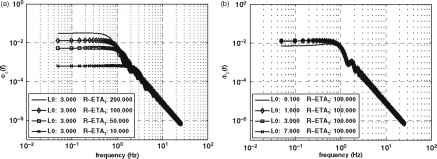
: 图1 (a)对数幅度spectra-showing变化在不同的R - n值,固定L0 = 3.0公里。(b)对数幅度spectra-showing变化在不同,固定的R - m = 100公里

发射机和接收机的预测速度矢量在平面垂直于洛杉矶是零。即预测是平行的。显然,这不是一般情况下,但对这种启发式分析这就足够了。接下来,考虑控股L0 n1固定和变化。中可以看到这个图1 b,参数值的R - n1 = 100公里和10 ={0.1,1.0,3.0,7.0}公里。从图1,很明显,在低频光谱对n1高度敏感,以减少灵敏度提高频率。可以看到从图1 b,它除了为10 = 0.1公里上气氛非常小的值对数幅度谱紊流长度尺度是相当不敏感。这些因素将重要的参数估计时。

3.2模拟研究和参数估计

调查进行参数估计,关注logamplitude光谱。假设接收信号样本是一个高斯过程,其频谱指数分布。利用这一事实,许多光谱可以生成的实现,即。,通过替换每个谱点样本从指数分布的随机数序列。一个例子是图2所示。仿真的目的是代表真实情况;因此,假设接收到的信号可以在50 Hz,价值和大约10年代的数据将进入一个光谱(512样本使用)。

对于这个练习,要估计的参数是C ^ ^ n。两例检查,(我)n1 L0固定和变化,和(2)控股L0固定和不同的n1。在每种情况下,单个参数最大似然(ML)方法被用来估计C2 (n1) ^ n。让@g (f) = p $ g (f);的下标g指的是函数(在这里,对数幅度谱)和p参数估计。在这种情况下,(f)是情商。(3)与Cl (n1) ^ n设置为1。然后给出一个测量或

图2理论对数幅度谱(黑色曲线),取而代之的是指数分布和值噪声(灰色点)

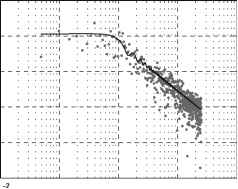
: 10 - 1 100 101频率(赫兹)

在这种情况下simulated-set谱点,(fi)、i = 1,……N p是由最大似然估计

的计算是通过一组完成N频率值(Smalikho 1997)。

图3说明了模拟结果的运动估计的C2 (n1)值,给定的固定(已知)n1,不同L0真实价值。图3 b中的数据,L0固定和n1是多样的。的“真”值L0和R - n1 3公里,100公里,分别。这对应于图1中的曲线与钻石的象征。灵敏度的概念是确定估计C2 (n1)给出一个不确定性知识的另外两个未知参数之一。即实现对数幅度谱生成给定的输入参数{C2 (n1), n1, L0}。这是< t 'x Eq (f)。(4)。该模型函数,(f),计算从情商。(3),(用C ^ (n1) = 1),使用相同的值的n1用于生成< PX (f);但L0值范围的固定值,用于生成x (f)。这些L0值构成的纵坐标图3。黑色的水平和垂直线条的真实值L0和C ^不会,分别。图3是一个二维直方图的{C; 2 (n1), L0}参数空间,用颜色代表的数量计数,本。 One thousand realizations, such as the one shown in Fig. 2, were generated for each L0 value. It can be seen that over a large range of length scales, the errors in estimating C2(n1)An are mostly within ±5% of the true value—the spread being dominated by the statistics of the random realizations. These results confirm the qualitative discussion above regarding the relatively insensitivity of the log-amplitude spectrum with respect to the length scale. That is, given a two-parameter model where one of the parameters is known, and it is insensitive to the other one, it is not surprising to see these results.

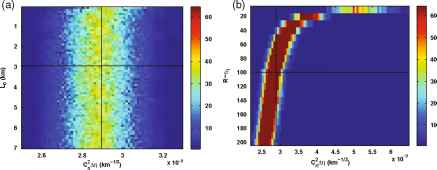
图3(一)分布的C ^ CniMn L0估计是不同的函数,当R - n1 =固定100公里。(b)的分布Cj2 (n1) ^ n估计的函数不同的R - n1,同时固定L0 = 3公里。黑色的水平和垂直线条的真实值L0和C ^ (n1),分别。注意,两个情节上的横坐标的规模是不同的

L0积极偏见是可见的最小值(10 = 0.1公里)。虽然这是一个有点不切实际的对流层上层的值,这种情况下的分析很有启发性。从图1 b,可以看出,在低频率,这个长度刻度值的范围大约是两倍小于频谱L0 = 3公里。回想一下,生成模拟频谱使用真实价值(3公里),是模型函数,给出错误的值(0.1公里)。指的是情商。(4),它可以看到高偏差发生的原因。错误长度尺度的模型频谱分为模拟谱,因为前者是在少数低频小点,ML估计量将产生一个小的正偏压。

图3 b说明了与上面相同的步骤,但是保持L0固定和不同的n1。为了方便起见,这个图的纵坐标是R - n1,来自接收者的紊流片之间的距离。黑色的水平和垂直线条的真实值R - n1和C ^ ^ n,分别。由于更大的敏感性频谱n1,偏见是在这种情况下更加明显。从图1,很明显,模型的谱点低频光谱与较小的R - n1价值(10公里)显著低于模拟谱(R - n1 = 100公里)。在10公里从低频值曲线的曲线100公里,有一个增加约20倍。从50 - 100公里曲线会导致增加约2.5倍。因此,越来越大的积极偏见减少R - n1值。这是出现在R - n1 < 100公里区域(黑水平线以上)图3 b。当然,情况恰恰相反:R - n1值用于模型谱比那些真正的增加(例如,模拟)光谱,偏差会越来越消极。 For example, in going from the low-frequency values on the 200 km curve to those on the 100 km curve, there is a decrease by a factor of around 2.5. This is seen in the R — n1 > 100 km portion of the figure.

对所有频率估计。在高频率估计。数据真实价值C2nδη

C„2 (km-1”3) x 10:9

:	所有频率的估计。在高频率估计。C数据真值δη
:



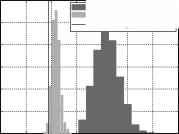
:		C2An (km-1 x„- 3)。 C2An (km-1 x„- 3)。图4 C的分布直方图;2 (n1) ML估计的值,使用logamplitude频谱。直方图的深灰色,所有的谱点是用于估计;只在浅灰色的高频率谱点使用。在这种情况下,R - n1的真正价值是100公里,模型值是10公里。(一)迭代之前使用n1估计,(b)使用n1估计迭代后偏差问题的部分解决方案是限制使用的谱点的ML估计高频区域,n1减弱的影响。这个练习的结果显示在图4。深灰色的直方图分布的C ^ (n1)估计,在1000年实现,使用所有的谱点。在这种情况下,一个值的R - n1 = 10公里用于模拟光谱模型谱而值为100公里。这对应于图3 b顶线,在那里可以看到有一个显著的正偏压,以及更广泛的分布。当使用的点集ML估计仅限于高频点,偏差和传播都显著降低。这可以在浅灰色的分布。输入C; 2 (n1)值由竖线表示。 3.3迭代参数估计从图4可以看到,仍然有一个非平凡的偏差估计的C2 (n1)即使限制使用的谱点ML估计那些在更高的频率值。它可以表明ML估计量的偏差成正比的右边Eq。(4), - 1。在更高的频率,情商的比率在右边。(4)小于那些在较低的频率,但有很多指向更高频率,以便这些比率可以显著的总和。这些比率的原因不是一个在这种情况下是n1不等于n。改善这种影响的一个方法是使用两步计算方法的估计^(不会。第一步是评估C; 2 (n1)在前一节中描述的方法。n1的价值是猜到了,和使用的ML算法。由于长度刻度值不是很相关的,选择一个合理的物理值。鉴于这两个参数,对数幅度谱现在n1单一未知参数的函数。最小二乘最小化方法用于估计n1,进而利用的“猜测”价值在第二个迭代ML估计的C2 (n1) ^ n。在这种情况下,R - n1的真正价值是100公里,模型值是10公里。 The n1 estimates computed from the minimization method have a high bias. This is due to the positive bias in the first estimates of C^nOAn. Referring to Eq. (4), if the C^(n1)An estimates are too large, then the model function, (f, i^), must be smaller in order to minimize the difference between the data, &g (fi), and the product of the C2(n1)An estimates and the model. Making the model function smaller implies that larger n1, or equivalently, smaller R — n1 values, must be used (cf. Fig. 1a). Note that since the true value of R — n1 is larger than the original model one, (100 km vs. 10 km); estimating larger n1 values should redu

继续阅读:的无线电掩星探测电离层空间天气应用成果和前景

这篇文章有用吗?

地球