土壤饱和电导率
即使一个严格的单维解,不考虑下游和横向毛细效应和尺度效应,大致代表了现场物理现象,我们尝试使用达西方法,特别是对于实验地点(Melezzo Occidentale河流域和安扎河流域),这些实验地点的水保持关系未知。
在调查案例中,通过观察,经过长时间的吸胀后,渗透仪周围的土壤可以被认为几乎饱和,在渗透仪下游假设有一个压头p/ym = D(见图9.1和章节9.2.2)。在实验室分析中验证了这一假设,验证了98%的土壤在改良水分入渗试验结束时达到饱和,其他土壤接近饱和。因此,将确定Ks的回归应用于修正-水分累积入渗曲线最后阶段的数据。
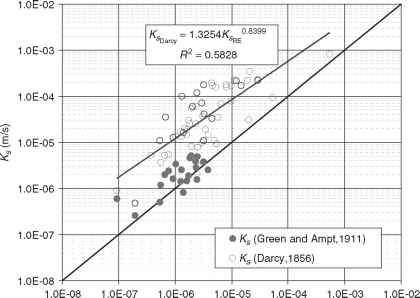
然后将该方法应用于Toce河和Mella河流域的上层土壤,并与GA法(Toce河流域)和RE法(Toce和Mella河流域)进行了比较。在图9.5中,土壤饱和图中表示了Toce河流域的电导率:可以看出,达西方法对Ks的估计平均比RE方法平均高约1个数量级。梅拉河流域土壤的饱和电导率也有相同的表现,回归系数R2 = 0.4705。另一方面,通过考虑润湿前沿的矩阵势(GA方法),即使使用单维表示也能更好地估计Ks。特别地,GA方法应用于自然水分累积入渗曲线的第一组数据(约15分钟的记录),直到可以假设该过程主要是单维的(详见9.2.2节)。另一方面,RE方法被应用于自然水分累积渗透曲线的最后一端,以便拥有一个几乎恒定的内部池塘的假设比测试开始时更加现实。由于在试验开始前采集了土壤样品,因此可以可靠地估计初始饱和硒。实验几何模型与作者提出的几何模型略有不同。
在实验室实验后估算的土壤饱和电导率与现场数据(GA法和RE法)之间发现了相当好的平均一致性,即使有很高的离散度(图9.6)。用渗透计测得的土壤体积和表面积比实验室测得的土壤芯大。因此,大孔隙更有可能包含在渗透计土壤中。然而,实验室和RE估计之间的系统性偏差并不明显。由于数据的高度分散和每种土壤类型的样本数量有限,不鼓励估计尺度因子的尝试(参见例如Focardi etal)。1997, Merz et al. 2002)描述了整个实验集。在图9.7中,表示了每个土壤类别(Toce河流域)的几何平均值,并比较了RE场法、达西法和实验室估发值。
类 |
Ks(米/秒) |
Ks(米/秒) |
Ks,马克斯(米/秒) |
Ks, mm(米/秒) |
Ks(米/秒) |
Ks(米/秒) |
Ks,马克斯(米/秒) |
Ks, mm(米/秒) |
||
达西(f) |
达西(J) |
(达西) |
(达西) |
(重新) |
(重新J) |
(重新) |
(重新) |
|||
不连续的城市肌理 |
3.68 e-04 |
(6) |
2.67 e-04 |
6.33 e-04 |
2.84 e-05 |
6.20 e-06 |
(6) |
4.11 e-06 |
1.55 e-05 |
7.04 e-07 |
种植和木质农业区域 |
9.78 e-04 |
(3) |
2.39 e-04 |
2.76 e 03 |
3.52 e-05 |
5.14 e-06 |
(2) |
3.54 e-06 |
8.87 e-06 |
1.42 e-06 |
草浸。碎石和坡底。 |
7.03 e-04 |
(6) |
3.45 e-04 |
2.27 e 03 |
1.85 e-05 |
8.83 e-05 |
(6) |
1.54 e-05 |
4.57 e-04 |
1.26 e-06 |
森林浸。碎石和坡底。 |
1.24 e 03 |
(11) |
7.46 e-04 |
2.58 e 03 |
1.67 e-05 |
1.59 e-05 |
(5) |
1.31 e-05 |
2.83 e-05 |
4.94 e-06 |
最近被草覆盖的冲积层 |
8.47 e-04 |
(7) |
6.73 e-04 |
1.58 e 03 |
1.72 e-04 |
2.81 e-05 |
(6) |
1.25 e-05 |
5.41 e-05 |
2.59 e-07 |
最近被森林覆盖的冲积层 |
6.71 e-04 |
(7) |
1.51 e-04 |
2.99 e 03 |
3.49 e-06 |
8.51 e-06 |
(5) |
3.08 e-06 |
3.22 e-05 |
2.50 e-07 |
草覆盖的淋积渣滓 |
5.96 e-04 |
(13) |
2.78 e-04 |
3.27 e 03 |
2.23 e-05 |
2.32 e-05 |
(10) |
8.32 e-06 |
1.36 e-04 |
8.01 e-07 |
森林覆盖的残积积渣 |
9.80 e-04 |
(3) |
5.73 e-04 |
2.35 e 03 |
2.19 e-04 |
9.51 e-06 |
(1) |
9.51 e-06 |
9.51 e-06 |
9.51 e-06 |
绿草覆盖的冰川 |
2.57 e-04 |
(3) |
1.84 e-04 |
4.07 e-04 |
4.88 e-05 |
4.54 e-06 |
(2) |
4.04 e-06 |
6.62 e-06 |
2.47 e-06 |
被草覆盖的冲积扇 |
1.26 e 03 |
(2) |
9.44 e-04 |
2.10 e 03 |
4.25 e-04 |
1.49 e-04 |
(1) |
1.49 e-04 |
1.49 e-04 |
1.49 e-04 |
森林覆盖的冲积扇 |
5.61 e-04 |
(2) |
5.51 e-04 |
6.67 e-04 |
4.56 e-04 |
3.67 e-05 |
(1) |
3.67 e-05 |
3.67 e-05 |
3.67 e-05 |
绿草覆盖的企业集团 |
1.25 e-06 |
(1) |
1.25 e-06 |
1.25 e-06 |
1.25 e-06 |
1.29 e-07 |
(1) |
1.29 e-07 |
1.29 e-07 |
1.29 e-07 |
森林覆盖企业集团 |
8.37 e-04 |
(2) |
6.90 e-04 |
1.31 e 03 |
3.63 e-04 |
2.43 e-05 |
(2) |
2.18 e-05 |
3.51 e-05 |
1.36 e-05 |
绿草覆盖的砂岩 |
1.18 e 03 |
(3) |
1.05 e 03 |
2.04 e 03 |
7.14 e-04 |
2.34 e-05 |
(2) |
2.34 e-05 |
2.35 e-05 |
2.33 e-05 |
草浸。石灰。, dolom。石灰。, dolost。 |
4.06 e-04 |
(3) |
3.96 e-04 |
5.37 e-04 |
3.20 e-04 |
6.95 e-06 |
(3) |
6.54 e-06 |
1.05 e-05 |
5.08 e-06 |
森林浸。石灰。, dolom。石灰。, dolost。 |
2.34 e 03 |
(5) |
1.87 e 03 |
5.12 e 03 |
5.74 e-04 |
5.52 e-05 |
(3) |
5.37 e-05 |
7.44 e-05 |
4.36 e-05 |
绿草覆盖的片麻岩 |
1.21 e 03 |
(3) |
1.69 e-04 |
3.33 e 03 |
4.78 e-06 |
3.18 e-06 |
(2) |
2.81 e-06 |
4.68 e-06 |
1.69 e-06 |
Ks (Reynolds and Elrick, 1991) (m/s)图9.5托采河流域部分土壤经现场数据估算的饱和电导率的比较
”
1.0 e 03
1.0 e-04
1.0 e-05
1.0 e-06
1.0 e-07
1.0 e-08
1.0 e-04
1.0 e-05
1.0 e-06
1.0 e-07
3 0 - |
||||||
O” |
h aVi 0* |
3 /♦ |
||||
•V |
1 * |
|||||
•阿 |
-♦ |
♦ |
||||
+ k (R•k (G k (D |
eynolds, E reen和Amp arcy, 1856) |
伊里克,1991)t, 1911) |
实验室数据后Ks (m/s) 1.0 e-04 1.0 e 03 图9.6 Toce河流域一些土壤的饱和电导率在现场和实验室数据后的不同估计的比较  图9.7托采河流域图土壤发生和土地利用等级的土壤饱和电导率不同估计值的比较 Ks(几何学。Av .)实验室数据后(m/s) 图9.7托采河流域图土壤发生和土地利用等级的土壤饱和电导率不同估计值的比较 为了表征上层土壤中水的行为,特别是在强降雨事件中,当表面土壤几乎饱和时,经过长时间的吸胀过程后,研究了土壤第一层的饱和电导率。土壤饱和电导率一般随上层土层的深度而减小。这一趋势是由于土壤表面的物理和化学过程改变了非完全腐烂的有机质和残积颗粒的不透水层的存在,以及土壤颗粒的质地更细。在这些野外活动中,通过比较上层和下层饱和电导率的估计,也发现了这些结果,这些结果通常由山坡水文模型(Beven和Kirkby 1979)假设。在图9.8中,使用表面饱和电导率归一化的下层Ks(达西法)显示了Melezzo Occidentale河流域和Anza河流域的土壤。因此可以预期,一旦土壤表面饱和,例如在强降雨事件结束时,土壤对降雨的响应主要受土壤饱和电导率较低的下层控制。 在模拟山坡径流响应时(Beven和Kirkby 1979, Kirkby 1985),通常假设饱和电导率随深度的指数衰减可用于拟合观测值: 其中z为正向上,如前所述,Ks(0)为表层土壤饱和电导率。从垂直饱和电导率的数据中,可以发现指数衰减常数1// = 0.19 m。这个值与Beven(1983)在27个土壤集上估计的饱和横向电导率衰减常数的范围(在0.2到0.4 m之间)一致。然而,数据的高度分散证明了由于不同的局部成土过程和土壤发育程度,单一层位深度的重要性。此外,这些不均匀性指出了在涉及研究区域的应用中,扩展山坡理论框架的困难径流过程到整个盆地。 最后,由于侵蚀、运输和沉积过程之间的竞争,随着海拔的增加,土壤预计会变得更粗,因此,主要由土壤颗粒之间的大孔隙引起的土壤饱和电导率预计也会增加。的  图9.8上层土壤饱和电导率对比(安扎河流域和西米利佐河流域土壤现场数据) 图9.8上层土壤饱和电导率对比(安扎河流域和西米利佐河流域土壤现场数据) 在实验室分析后估算出的Toce河流域土壤的饱和电导率与实验地点的海拔高度之间的关系。与意大利阿尔卑斯中部的另一个山地盆地(Orlandini et al. 1999)报告的结果定性一致,图9.9中可以观察到,随着海拔2000米的增加,土壤饱和电导率增加了约1个数量级。虽然数据的分布范围非常大,但Ks对数与海拔的回归曲线的斜率和相关性均不为零,且具有0.05的显著性。 |
|||
继续阅读:问ssSfc
这篇文章有用吗?