植被拦截
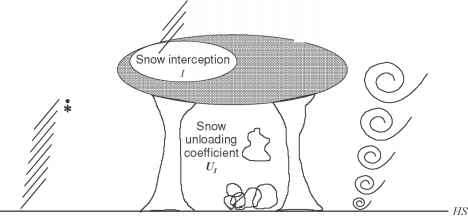
植被截留雪是其冬季叶、茎面积和降雪事件大小的函数。由于升华和融化将雪从冠层中移除,因此拦截(被困在冠层中的降雪,通常基于事件)与雪负荷(特定时间冠层中的雪)是不同的。Hedstrom和Pomeroy(1998)开发并实地测试了如下形式的雪拦截和雪卸载模型(见图3.3):
I = he-U 't h = (ll - ll,o)(1 - eccanP/ ll)
大气
降水率
树冠
* (q)/升华和蒸发速率
大气
降水率
树冠
* (q)/升华和蒸发速率
积雪
单位面积的雪量
积雪
单位面积的雪量
图3.3。植被拦截和卸载。
式中,I为卸载发生后的截雪量(kg m-2), I1为卸载开始时的截雪量,UI为卸雪系数,t为时间(s), LL为最大冠层雪荷载,LL,o为初始雪荷载,P为累计降雪量(kg m-2), ccan为冠层闭合。
Hedstrom和Pomeroy(1998)利用周时间分辨率的经验数据,在南方北方森林中发现e~Ult = 0.678。可以使用Schmidt和Gluns(1991)开发的经验关系来确定LL,其中:
LLb为单位树枝面积最大雪荷载(kg m-2), ps为密度新鲜的雪(kg m-3), LAI为冬季叶茎面积指数(m2 m-2)。LLb范围从云杉的5.9 kg - m-2到松树的6.6 kg - m-2。式(3.28)是对Calder(1990)提出的表达式的扩展,该表达式基于降雨拦截所用的公式。与早期公式的重要区别在于考虑冠层雪荷载降低拦截效率,并且与最大降雨量拦截相比,发现的最大冠层雪荷载相当高。密集针叶树冠层的拦截效率(I/P)从很小的值到0.6不等,并且随着风暴降雪量和初始冠层雪负荷的增加而下降。
冠层中的雪代表了一个“雪面”,与地面上的雪有着非常不同的特征(Harding and Pomeroy, 1996)。例如,它相对较好地暴露于大气并受到高净辐射,因为积雪覆盖的冠层保持其低的无雪反照率(Pomeroy和Dion, 1996;Yamazaki et al., 1996),在空气动力学上是粗糙的(Lundberg et al., 1998),并且通常与稍微不稳定的表面边界层有关(Nakai et al., 1999)。不同的雪荷载及其在冠层中的暴露程度意味着积雪覆盖的冠层不表现为连续的,饱和的表面;这影响了树冠中水分的自由可用性。Nakai等人(1999)通过改变体积传递系数Cq / CH的比率(见式3.12)来解释这种影响,从低水分情况下的0.1(低雪荷载)到高水分情况下的1.0(高雪荷载)。Lundberg等人(1998)使用Penman-Monteith组合模型和阻力参数化来估计积雪冠层的升华,并发现积雪冠层的阻力必须设置为雨覆盖冠层的10倍,才能提供与测量结果相匹配的结果。Parviainen和Pomeroy(2000)采用了一种耦合计算方案,通过计算来自雪团的湍流转移(假设无雪冠层没有蒸发)来提供冠层内的湿度和温度场,然后将其与整个冠层的体积转移公式相匹配,如式(3.11)所示。既明智又潜热传递由式(3.11)的变式计算得出,其中CH和Cq分别用Chq代替,u (z)分别用Sherwood数和Nusselt数代替,用于粒子的热和水蒸气的湍流传递,并在假设升华的雪团在冰球表面温度下处于热力学平衡状态下求解(Schmidt, 1991)。Chq为:
式中,Ll为雪荷载(等于初始拦截,I1,减去任何升华和卸载),kci为无因次雪团形状系数,rpt,n为标称雪粒子半径(0.0005 m), pi为冰的密度(kg m-3), x I比拦截雪的分形维数小1.0 (Pomeroy and Schmidt, 1993)。Pomeroy等人(1998a)发现成熟常绿植物的x I通常为0.4,Parviainen和Pomeroy(2000)报告经验推导出加拿大西部成熟针叶林的kcl值(给定名义rpt,n)为0.0114,幼龄针叶林为0.0105。
大气
*降水率
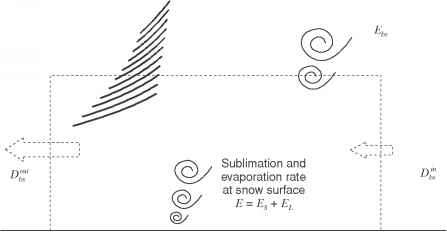
吹雪升华率
大气
*降水率
吹雪升华率
吹雪运输
积雪
单位面积的雪量
吹雪运输
积雪
单位面积的雪量
继续阅读:高山地形堆积
这篇文章有帮助吗?