雪中相平衡热力学

散装平衡温度在一个纯粹的水系统

三种水相之间的热力学关系决定了晶粒的生长雪的变质．化合物H2O是以冰、水还是水蒸气的形式存在，取决于其温度(T)和压力(p)，如图2.5相图所示。蒸发(A)、升华(B)和熔化(C)的曲线描绘了两个体积-水相在热力学平衡中共存的点。三相共存于三相点，温度为0.01℃，蒸汽压为6.1112 hPa。雷竞技csgo这和普通不一样冰的熔点，在0°C和1个大气压(1013.25 hPa)的温度下发生。蒸汽沿虚线A'相对于过冷水处于亚稳态平衡，这将蒸发曲线延伸到0.01°C以下。

在平衡状态下充满蒸汽的空气是饱和的，更多蒸汽的加入会引起冷凝。在三点以下，饱和蒸汽压相对于水的平衡总是超过相对于冰的平衡，因此有利于雪晶体的生长，如2.1.2节所述。过量饱和蒸汽压在-11.8°C时达到最大值(见图2.5)。蒸汽相对于水的过饱和从0°C时的0%增加到-40°C时的46%。

相图中的曲线是通过积分确定的克劳修斯——克拉珀龙方程方程dp Lji

其中i和j是两个相，T是开尔文，V是单位质量相的体积(或倒数密度)，L是潜热。在0°C时潜在的热融合(Lie)、蒸发(L¿v)和升华(Liv)分别为3.335 × 105、2.505 × 106和2.838 × 106 J kg-1。L适度地依赖于温度(见Pruppacher和Klett, 1997, p. 97)。对于理想气体和恒定Lkv，式(2.1)的积分提供了形式的蒸发和升华曲线的近似表达式

T的单位是°C。这里，pvsat,k是相对于冰或水的饱和蒸汽压(hPa)，系数a, b和c是给定的经验拟合温度范围．对于-40到0°C之间的范围，Buck(1981)推荐使用该表达式

pv。Sau = [1.0007 + (3.46 x 10-6pa)]6.1121 expf ^ \ (2.3)

pv,坐,我= (1.0003 + (4.18 x 10-6pa)) 6.11雷竞技csgo15 exp(——)(2.4)

在-50到0°C之间的水饱和度

为冰饱和度，其中pa为大气压(hPa)。两个表达式中的初始系数都是一个轻微的修正因子，用于气相是湿空气而不是纯水蒸汽。

曲率对雪中相平衡的影响克劳修斯-克拉珀龙方程为被平面分离的相。当表面弯曲时，这些平衡条件就会改变，就像冰粒或半月板中的水一样湿雪(图2.4)。由于需要做功来扩展界面薄膜，凸界面后面的相经历了更高的能量和压力。通过曲面的压差(pij = pi - pj)由拉普拉斯方程给出为pj = -1， (2.5)

其中a j为界面表面张力，Z ij为平均曲率半径(Defay et al.， 1966, p. 6 Dullien, 1992, pp. 119-122)。表面张力a^， aiv，

表2.3冰球饱和压力与平面饱和压力之比。

表2.3冰球饱和压力与平面饱和压力之比。

Rg (1 × 10-3	米)	10 - 6	纯	10-4	三分	10 - 2	10 - 1
pv,坐,我/ pv,坐,我	0°C	6.05	1.20	1.018	1.002	1.0002	1.000 02
-20°C		6.97	1.21	1.020	1.002	1.0002	1.000 02

和oag在0℃时的平均值分别为0.028、0.104和0.076 Nm-1，且随温度变化较大(Pruppacher, 1995)。更高的表面张力和更紧的曲率导致较大的压力差异．

对于曲面，克劳修斯-克拉珀龙方程推广到吉布斯-杜赫姆方程(Defay et al.， 1966, Colbeck, 1980)

Gibbs-Duhem方程通过拉普拉斯方程将相压联系起来，积分为曲面上的平衡蒸汽压p'vsat k的开尔文表达式

“2 okv 1

Pv,sat, k_ Pv,sat, kexp

这里pv sat k是平面上的平衡压强，pk是水的密度或者冰，Rv是气体常数是水蒸气(= 461.50 jkg - 1k -1)， T单位为开尔文。由式(2.7)可知，冰粒越小或结构越细，曲率越高，蒸汽压越高。表2.3显示了p!v sat k/pv sat k对于不同半径的冰球(Z±v = rg)在0和-20°C的温度。

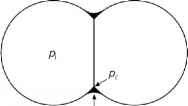
Gibbs-Duhem方程也预测了融化雪的温度．在两相水-冰系统的情况下，例如饱和水雪或包内的饱和水雪袋(图2.6a中的颗粒a)，水中的压力由毛细压力计算，pat = pa - pt，而冰中的压力则由拉普拉斯方程计算。我们在第2.4.2节讨论毛细管压力。饱和水雪的熔点降低与毛细压力成正比，与颗粒半径成反比

273.15

2欧六世的

因此，较大的冰粒具有较高的融化温度，并以较小的冰粒为代价生长。在完全饱和的积雪中，空气/水界面是平坦的，式(2.8)中的第一项消失。

在含水量较低时，液体通常呈两粒接触的摆环状，或呈三粒簇的脉状，如图2.6b和c r g所示

Ca«Pa

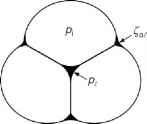
图2.6。湿雪中水夹杂物的压力关系和形状，其中pk为压力，Z ai为空气/水界面的曲率半径。(a)雪中含水量高(不结垢)的饱和区。(b)在低含水量的雪中与摆状夹杂物的双颗粒接触(转载自Colbeck, 1979;版权1979年，由爱思唯尔授权)。(c)在低含水量的雪地中，三粒簇状脉状夹杂物(转载自Colbeck, 1979，见b)。

(Colbeck, 1979)。由于空气占据了大部分孔隙空间，冰中的压力计算从拉普拉斯方程应用到冰/空气界面，熔点下降为(Defay et al.， 1966;Colbeck, 1979)

273.15

2 ctw六世

由于(2.9)中的第二项较小，因此Td主要取决于毛细管压力，毛细管压力随液态水的减少而增加。

由式(2.8)和式(2.9)预测的熔化温度仅略低于0°C的体值，因此，对于能量平衡计算，表面张力和曲率对温度的影响不显著。然而，他们是最重要的雪变质还有粘结强度。在含水量较低的情况下，颗粒表面的融化温度低于冰键的融化温度，将热量从冰键中引导出来，导致它们生长和加强(Colbeck, 1979)。当雪粒完全被水包围时，就会发生热力学逆转热量流动向化学键靠近，导致化学键融化。因此，雪中的饱和或“泥状”区域是无内聚的，具有很小的r g强度。融水中的杂质通过KfM进一步降低了融化温度，其中KF (=1.855 K kg mol-1)是水的冷冻常数，M是物质的质量摩尔浓度(每千克溶剂中溶质的摩尔数)。

继续阅读:雪变质

这篇文章有用吗?

0 0