第一眼看到失控的温室

我们在第二章中已经看到，大气与凝结物(如海水)相平衡的质量不是固定的。它随着温度的升高而升高，这与温度的要求是一致的克劳修斯——克拉珀龙方程关系。如果可冷凝物质是温室气体，则光学厚度随温度而增加。这往往会降低OLR，抵消甚至扭转温度上升增加OLR的趋势。这对OLR对表面温度的依赖性有什么影响行星能量平衡？由此产生的现象通常被认为与水海洋对行星气候演变的影响有关，但这一概念可推广到任何与大型冷凝储层处于平衡状态的可冷凝温室气体。raybet雷竞技最新我们先来看看这个问题，在灰色气体模型的背景下。

在一般情况下，我们想要考虑这样一种大气:在这种大气中，可冷凝的温室气体与质量固定的不可冷凝的背景气体混合在一起(后者本身也可能有温室效应)。地球大气中的水蒸气、土卫六上的甲烷都是如此，金星早期大气中的水蒸气可能也是如此。这也可能是早期火星上氮-二氧化碳混合大气的情况，二氧化碳扮演着可冷凝成分的角色。我们最终将讨论这样的大气，但是计算双组分大气的湿绝热的困难引入了一些干扰，阻碍了对关键现象的理解。因此，我们将从更简单的情况开始大气由与蓄水池(“海洋”或冰川)平衡的纯可冷凝组分。在这种情况下，饱和湿绝热曲线由简单的解析公式Eq. 2.27给出，通过求解简化形式得到克劳修斯——克拉珀龙方程温度与压强的关系。我们已经在第二章中看到，在大温度下，混合大气是由可冷凝成分主导的，所以如果我们主要对大温度行为感兴趣，使用单组分可冷凝气氛是一个很好的近似。

我们写T(p) = To/(1 -■RT0 ln pp)，其中(po,To)是饱和曲线上固定的参考温度和压力，如三点温度和压力。如果表面压力为ps，则表面温度为Ts = T(ps)。因此，在这个问题中，指定表面压力相当于指定表面温度。为了保持代数简单，我们假设一个常数的特定吸收«。然后= Kps/g，随着Ts变大而增加。此外，对于恒定比吸收，p/po = (tto - t')/ro，其中To =«po/g。现在，参考温度和压力(po,To)的选择是完全任意的，无论我们做出什么选择，我们都会得到相同的答案(在我们使用的克劳修斯-克拉珀龙近似形式的精度范围内)。因此，我们可以自由地设置po = g/«，以便to = 1。然后，To隐式地依赖于«，并且随着«变小而变大。To是相对于大气顶部测量的光学深度为单位的大气高度的温度。

将单分量T(p)代入积分得到史瓦西方程，用光学厚度代替压力，我们发现

在第二行中，我们像以前一样定义了一个新的虚拟变量t1 = t0 - t'。表面温度仅通过t0进入OLR表达式，t0与表面压力成正比。在光学薄极限下，表达式右边的积分很小(因为t0很小)。这发生在表面温度较低的情况下，因为当表面温度较小时，ps也较小。然后OLR减少到第一项，约为1+(0)，即。来自地表的未修改的向上辐射。在光学厚度极限下，发生在高表面温度下，与1+(0)成比例的项可以忽略不计，而第二项占主导地位。这一项由通量aT4乘以一个无维积分组成。回想一下，To是一个常数，依赖于构成大气的气体的热力学和红外光学性质;它不随表面温度变化。 Because of the decaying exponential in the integrand, the integral is dominated by the contribution from the vicinity of t1 = 0, and will therefore become independent of t0 for large t0 1. In the optically thick (high temperature) limit, then, the integral is a function of RTo/L alone. From this we conclude that the OLR becomes independent of surface temperature in the limit of large surface temperature (and hence large t0). This limiting OLR is known as the Kombayashi-Ingersoll limit. It was originally studied in connection with the long-term history of water on Venus, using a somewhat different argument than we have presented here. We shall use the term to refer to a limiting OLR arising from the evaporation of any volatile greenhouse gas reservoir, whether computed using a grey gas model or a more realistic radiation model.

当RTo/L趋近于零时，aT^的积分趋近于一是很容易证明的。事实上，对于典型的大气气体，L/R是一个非常大的温度，在几千开尔文的数量级上。因此，除非比吸收非常小，否则RTo/L趋于小，通常在.1或更小的数量级。当RTo/L = .1时，积分值为.905。因此，极限OLR本质上是aT^。回忆To是从大气顶部向下一个光学深度单位处的湿绝热层的温度，我们看到极限OLR的行为非常接近于所有长波辐射都是从大气顶部向下一个光学深度单位的层发射出来的。

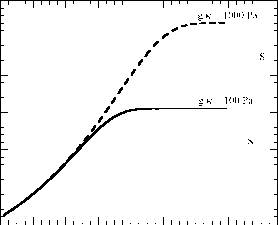
图4.3显示了对方程4.38中的积分进行数值计算的一些结果。地表温度小，大气少，OLR随at4增大。随着地表温度的增大，大气变厚，OLR最终渐近于一个极限值，正如预测的那样。根据上面给出的论证，极限OLR应略小于从大气顶部向下一个光学深度找到的温度所对应的黑体通量。这个温度取决于g/K，也就是从顶部向下一个光学深度的压强。对于g/K = 100Pa，求解T在100Pa时的简化克劳修斯-克拉珀龙关系得到T0 = 250.3K，其中aTo4 = 222.6W/m2;g/K = 1000Pa时，To = 280.1K, aT04 = 349.0W/m2。这些数值与图中数值结果一致。

注意，对于给定的大气成分(决定k)， Kombayashi-Ingersoll极限取决于重力加速度。表面引力较强的行星将比重力较弱的行星具有更高的Kombayashi-Ingersoll极限。用单组分饱和绝热的公式(式2.27)代入To，得到了对g/K的依赖关系的显式公式。因此，极限OLR可以写成这样的形式

OLRo = A(L/R)aT04 =¿(L/R^LR^ (4.39)

其中A(L/R)是前面讨论过的顺序单位常数，p* = pref exp(L/RTref)。严格来说，积分在很大的r^处发散，因为被积函数的分母可以消失。这是假定潜热恒定的假象，没有物理意义。

350 300

E 200

100年50

180 200 220 240 260 280 300 320 340表面温度

图4.3:与储层平衡的单组分灰色气体可冷凝大气的OLR与表面温度的关系。计算了水蒸气对应的热力学参数L和R。结果显示了两个不同的g/K值，其中K是气体的特定横截面，g是重力加速度。

p*， (pref, Tref)的公式是饱和蒸汽压曲线上的任意点，例如三点温度和压力。p*是一个巨大的压力(水蒸气为2.3•1011Pa)，因此公式4.39预测Kombayashi-Ingersoll极限随着表面重力的增加而增加，因为增加g会使分母上的对数变小。当Kp*/g = 1时，表观奇点是假的，因为我们所做的近似值在达到这个值之前就失效了。

我们现在准备描述失控的温室效应现象。设S为吸收的太阳辐射如果S < OLRmax，行星将以通常的方式达到平衡，直到它以与从恒星接收能量相同的速率通过红外辐射失去能量为止。但是如果S > OLRmax呢?在这种情况下，只要仍有海洋或其他凝结的储层向大气中输送物质，无论地球变暖多少，它都无法摆脱所接收到的所有太阳能;因此，地球继续变暖，直到表面温度变得如此之大，以至于整个海洋都蒸发到大气中。此时的温度取决于挥发性储层的质量和组成。例如，地球上的海洋含有足够的质量，如果以水蒸气的形式倾倒到大气中，可以将表面压力提高到100巴左右。当饱和蒸汽压达到这个值时，海洋已经枯竭。利用克劳修斯-克拉珀龙关系的简化指数形式，从海平面沸点(373.15K时为1巴)推断出蒸汽压，我们估计该蒸汽压是在表面温度约为550K时获得的。这个估计是不准确的，因为蒸发潜热在涉及的温度范围内有明显的变化。根据对蒸汽性质的测量，一个更精确的数值是584K，但我们所知道的蒸汽对生命生存或出现的严峻影响在很大程度上是相同的。

350 300

180 200 220 240 260 280 300 320 340表面温度

海洋体积

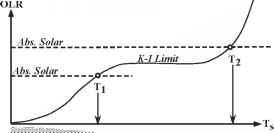
图4.4:挥发性储层枯竭时失控温室终止的示意图。

当温度高于海洋枯竭时，大气的质量变得固定，不再随温度而增加。大气中的温室气体含量——在目前的情况下是整个大气——不再随着温度而增加。结果，随着地表变暖，OLR再次自由增加，地球将变暖，直到在比海洋枯竭时更高的温度达到平衡。所需的额外增温取决于Kombayashi-Ingersoll极限和吸收的太阳辐射之间的差距。这种情况如图4.4所示。一旦海洋消失，低层大气就不饱和了，空气可以在凝结发生之前被抬升一段距离。由此产生的大气廓线位于低层大气的干绝热区，在冷凝开始的高度过渡到湿绝热区。这种情况与图2.6中二氧化碳所描述的情况相同。在凝结层中仍然会形成雨。大部分将在较低的非冷凝层蒸发; some of it may reach the ground, but the resulting puddles would tend to rapidly evaporate back into the highly undersaturated lower atmosphere. As surface temperature is made larger, the altitude where condensation sets in moves higher, until at very large temperatures the atmosphere behaves like a noncondensing dry system (albeit one where the entire atmosphere may consist of water vapor).

失控的温室效应现象或许可以解释，尽管金星一开始的状态与地球相当相似，但为何最终会出现与地球截然不同的气候。raybet雷竞技最新标准的说法是这样的:金星一开始是海洋，和地球一样，金星的大部分二氧化碳都凝结在岩石中。然而，它离太阳的距离已经足够近，足以引发失控的温室效应。一旦整个海洋蒸发到大气中，高层大气中就有如此多的水蒸气，以至于可以被高能太阳能分解紫外线，然后轻氢可以逃逸到太空中。留下的高活性氧会在表面反应形成矿物质。一旦不再有液态水存在，将二氧化碳结合在岩石中的反应就不能再发生了(这将在第八章中解释)，所以地球上所有的二氧化碳都从火山活动中释放出来，留在大气中，形成了现代金星的热而干燥的超高密度大气。

假设宜居性需要液态水的储存库，那么水的kombayasi - ingersoll极限决定了宜居性的内轨道极限，因为如果太阳常数超过了极限通量，就会发生失控，任何初始海洋都不会持续存在。它还决定了地球的太阳亮度达到足以引发失控所需的时间，从而确定了依赖水的生物圈(包括地球)的寿命。因此，精确计算kombayasi - ingersoll极限对于理解时间和轨道位置上的宜居性极限至关重要。灰色气体模型不能很好地确定适合于给定气体的po值，因此不能用于温室失控阈值的准确评估。我们至少可以说，在其他条件相同的情况下，表面引力较大的行星不太容易受到失控温室效应的影响。这是因为po = g/«，其中更大的g意味着更大的po，这反过来意味着更大的T(po)，因此更大的极限OLR。这一观察结果可能与类有关太阳系外行星被称为“大地球”。

我们将在第4.6节中使用更现实的辐射物理学来重温失控的温室。平流层效应和云效应的一些效应将在第五章中讨论。

温室气体失控现象通常被认为与水蒸气联系在一起，但这一概念同样适用于任何有挥发性温室气体储层的情况，无论是固态还是液态。例如，一个失控的温室可能与一个大的二氧化碳冰帽的升华有关，或者与甲烷或氨海洋的蒸发有关。事实上，Kombayashi-Ingersoll极限决定了一颗行星是否会在其表面(冰川或海洋)形成凝结物质的储层，前提是在没有任何化学汇的情况下，这种物质会持续排出气体。随着气体在大气中积聚，压力增加，最终会在地表凝结，阻止任何进一步的气体积聚。然而，气体的温室效应使地表变暖，从而增加了饱和蒸汽压。Kombayashi-Ingersoll极限告诉我们，当表面压力增加时，哪种效应会胜出。地球低于水的临界值，所以我们有一个水海洋。金星高于水和二氧化碳的阈值，所以两者都以气体的形式在大气中积累(除了可能逃逸到太空)。当我们用real-重新审视这个问题时气体辐射在没有化学汇的情况下，我们将能够确定二氧化碳是否会在地球、火星或土卫六上形成一个冷凝的储层。

继续阅读:灰色气体大气的纯辐射平衡

这篇文章有用吗?

0 0