入射太阳辐射的分布
温度的地理变化是由照射在每平方米表面上的阳光量的变化和反照率的变化所驱动的。季节变化是由地球在轨道上运行时吸收的阳光的地理分布的变化所驱动的。因此,任何处理季节和地理变化的出发点都必须是研究行星太阳的光如何分布在行星的球面上。本节只讨论入射阳光或日照的分布。阳光吸收量的地理分布也受到反照率分布的影响。反照率的变化也会通过冰的季节性变化影响太阳强迫的季节性分布,雪,云还有植被覆盖。
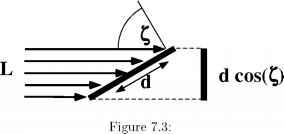
首先考虑一个没有空气的星球会有帮助,这样我们就不必马上去处理那些可能发生的事情散射效应大气对太阳光束的影响。如果我们的星球离它的太阳很远,与太阳的半径相比,照射到行星上的阳光是一束通量为l的平行射线。即使行星的表面完全吸收阳光,行星所拦截的阳光也不会均匀地分布在它的表面;如图7.3所示,按单位面积计算,地球上太阳直射的部分能接收到大量能量,而太阳以较浅的角度从地球表面掠过的部分只能接收到很少的能量,因为被拦截的少量阳光分布在相对较大的面积上。当然,地球的黑夜面不会收到任何信号太阳能在所有。
的分布的一般表达式入射太阳辐射以单位表面积为单位,我们可以把地球表面分成许多小三角形,并分别考虑每个小三角形。被三角形拦截的太阳能是由三角形在垂直于太阳光束的屏幕上投射的阴影面积决定的。要计算这个面积,假设三角形的一个顶点位于
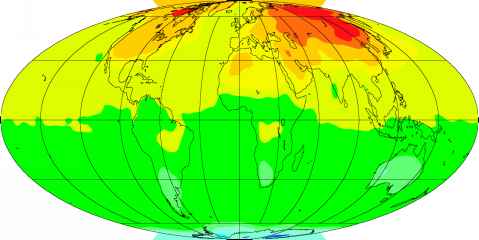
图7.2:7 - 1月地面空气温差图。
图7.2:7 - 1月地面空气温差图。
根据叉乘的定义,三角形的面积由2An = (rl x r2)给出,其中n是三角形所在平面的法向单位。为了得到三角形投影的阴影面积,我们对向量r{和r2在平面上的投影进行叉乘。这些投影由f\ - zr\•z和r2 - zr2•z给出,其中z是指向太阳方向的单位矢量。这两个向量的外积是
(rl - zr{•z) x (r2 - zr ^•z) = r (x r2 - (z x r2) (r (z) - (rl x z) (r2•z) (7.1)
现在,xy平面上两个向量的叉乘必须指向z轴的方向。因此,我们可以通过取上面向量与z的点积来得到上面向量的大小。这非常方便,因为zz与后两项的点积消失了,剩下的是
2A±= z•(rl × r2) = 2Az•n = 2A cos(z) (7.2)
其中,A±是阴影的面积,Z是表面的法线与太阳方向之间的角度。这就是天顶角。当天顶角为0时,太阳直接在头顶上,当天顶角为90度时,阳光与地面平行,不会留下任何能量。天顶的角度大于90o是非物理的,因为它们代表光必须穿过行星的固体主体才能照亮表面的下面;这些都是在地球的夜间。如果有人从行星的中心到太阳的中心画一条线,在这条线与行星表面相交的地方,天顶角将为零;这是太阳下点。在任何给定时刻,天顶角不变的曲线以亚太阳点为中心形成一组同心圆,天顶角为90°,沿该大圆在给定时刻将行星的昼侧和夜侧分开。如果表面与瞬时入射太阳通量处于平衡状态,那么太阳下点将是地球上最热的点,温度随着距离热点的距离而下降到零。当行星在它的昼夜循环中旋转时,表面的一个给定点被从热点扫过一段距离,导致一个白天的温度变异。当这颗行星在一年中沿着轨道运行时,随着行星旋转轴相对于太阳的方向的变化,日循环也会发生变化。只要地表实际上需要有限的时间来升温或降温,日循环就会在某种程度上减弱。
作为走向现实主义的下一步,现在让我们考虑一个快速旋转的行星,它的旋转轴垂直于连接行星中心和太阳中心的直线。如果旋转轴实际上垂直于轨道平面,这种情况一年四季都存在;否则,条件只在二分点处满足,并且条件确实定义了二分点。我们假设地球旋转得足够快,太阳辐射的昼夜差异被平均掉,相应的温度波动很小。换句话说,与地球表面的特征热响应时间相比,假定一天的长度较短,这一概念将在7.4节中定量探讨。如果a是行星的半径,那么这条行星表面的面积是2na2 cos(^)d^,如果角度是用弧度来测量的。的截面面积从太阳上从侧面看的光带的大小决定了光带所拦截的太阳通量的大小。这个面积是2a2cos2 (^)d^当d^很小时。因此,在纬度^的单位面积入射太阳辐射为lcos (^)/n。在赤道,单位面积的太阳辐射为L/n,略大于我们在第三章中通过平均整个地球表面的太阳辐射得到的L/4。如果地球上没有大气来传输热量或产生温室效应,那么地球就会变暖平衡温度是纬度的函数
赤道的温度最高,两极则降至零度。
对于上述几何情况,推导出天顶角余弦随经纬度的函数表达式。重新推导日平均分布的表达式太阳能吸收通过平均天顶角余弦沿纬度圈。
现在我们转向一般情况,在这种情况下,行星的旋转轴不垂直于包含轨道的平面。轨道平面的垂线与行星旋转轴之间的夹角称为倾角,我们称它为7。它可以被认为是一颗行星一年中的常数,尽管有更长期的变化,我们以后会感兴趣。现在的任务是确定太阳天顶角作为纬度、沿纬度圈的位置和一年中的时间的函数。
设点P是行星的中心,点S是太阳的中心。如果我们从P到S画一条线,它将在纬度5处与行星表面相交,这被称为太阳纬度,有时也称为亚太阳纬度。它仅仅是地球轴方向的函数,并作为我们在季节行进中所处位置的特征。如果行星的倾角是7,那么5的范围是北半球夏至时的7到夏至时的-7南半球夏季冬至。假设Q是地球表面的一个点,其特征是纬度$和“小时角”h, h是相对于当地中午(最高)的经度的经度太阳的位置)正在全球各地发生。为了辐射的目的,我们只需要计算天顶角Z,之前定义的。为了得到天顶角,我们只需要取向量QS和向量PQ的向量点积。要做到这一点,可以方便地引入一个以P为中心的局部笛卡尔坐标系,z轴与旋转轴重合,x轴位于包含旋转轴和PS的平面上,y轴与其他两个正交,选择完成右手坐标系。
首先,注意根据点积的定义,
继续阅读:Pq Pq Pq Ps Pq Ps cosZ Pqqs Pqqs Pqqs
这篇文章有用吗?


