OLR AaT p14 AaLR4494
~ ypV [ln (p* J \f20gsJKo)\ 4v;
检查图4.37中计算的Kombayashi-Ingersoll极限的g相关性表明,在1m/s2 < g < 100m/s2范围内,如果我们取A' = .7344和ko = .055(假设po = 104Pa),数值计算的相关性几乎完全可以用这个公式拟合。虽然吸收的压力依赖性导致极限OLR随g的变化比恒定k的情况更慢,但在真实气体情况下的极限表现非常像一个等效的灰色气体,ko = .055。考虑到实际气体吸收光谱的复杂性,这是一个令人惊讶的结果。等效吸收与表征2500 cm-1连续介质的等效吸收相似,这一事实表明极限OLR主要是由这个连续介质控制的。因此,这种连续体的行为对失控的温室现象(见问题??)。当温度升高到非常高的温度时,不能排除其他连续性可能会影响OLR。例如,波数大于5000cm-1的黑体总辐射在500K时仅为1.14W/m2,因此在500K或更低时,光谱中这部分的吸收性质无关重要。然而,当温度提高到600K时,短波发射为15W/m2,因此短波吸收开始起作用;由
320 300
pi eR 280
260 240
260 280 300 320 340 360 380 400表面温度(K)
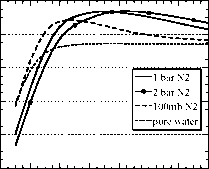
图4.38:对于图4.37,除了饱和湿绝热曲线上N2的水蒸气混合物。在地表重力为20m/s2的条件下,计算地表N2分压的指示值。
当T达到700K时,短波黑体发射为106W/m2,短波发射特性可能是重要的。另一方面,在这样的温度下,有很多大气中的水蒸气非常微弱的吸收就足以消除对OLR的贡献。
用应用于普朗克函数的数值求积法验证前段所给出的短波黑体发射数。
计算火星上水蒸气的Kombayashi-Ingersoll极限,g = 3.71 m/s2。计算土卫六(g = 1.35m/s2)和木卫二(g = 1.31m/s2)的极限。
现在让我们推广计算,引入一种不凝结的背景气体它在红外线下是透明的;在这个例子中,我们使用N2,尽管如果我们使用任何其他双原子分子,结果实际上是相同的。背景气体对Kombayashi-Ingersol极限的影响有两个方面:第一,压力加宽增加了吸收,这将降低极限。其次,背景气体使干绝热递减率比单组分饱和绝热递减率陡得多;原则上,递减率的增加可以增强温室效应,但考虑到水蒸气的可凝结性,它实际上减少了温室效应,因为高空的低温会急剧减少那里的水蒸气量。如果背景气体本身就是温室气体,那么这种效应的表现可能会大不相同。在足够高的温度下,水蒸气将主导背景气体,因此高温下的极限OLR将接近图4.37所示的纯水蒸气极限。然而,对于中等温度,背景气体可以改变OLR曲线的形状。
不同N2浓度下的结果如图4.38所示。像预期的那样。在较大温度下,极限OLR逐渐接近于纯水蒸气大气的值。这在大气中只有100MB N2的情况下尤其明显;随着N2的增加,在水蒸气完全支配OLR之前,人们必须达到更高的温度,但是
260 280 300 320 340 360 380 400表面温度(K)
图4.38:对于图4.37,除了饱和湿绝热曲线上N2的水蒸气混合物。在地表重力为20m/s2的条件下,计算地表N2分压的指示值。
趋势很明显。与纯水蒸气情况的一个非常重要的定性区别是,二元混合物的OLR曲线在中间温度下显示出一个明显的最大值。这一最大值的出现是因为水汽吸收特征的外部展宽相对较弱,而非冷凝背景气体的存在使递减率变陡,并减少了高空水汽的数量。曲线上的驼峰意味着表面温度在给定条件下呈现多重平衡吸收的太阳辐射.例如,100mb的N2,如果吸收的太阳辐射为320W/m2,则存在Tg = 288K的冷平衡和Tg = 360K的热平衡。后者是不稳定平衡;将温度向冷方向转移将导致水蒸气凝结,OLR降低,进一步冷却气候,直到系统进入冷平衡。raybet雷竞技最新相反,将温度稍微移向热平衡的较暖一侧,将导致气候进入失控状态。raybet雷竞技最新对于这些大气参数,行星处于亚稳态失控状态。除非某个raybet雷竞技最新短暂的事件使地球变暖到足以让它进入失控状态,否则气候将持续处于较冷的、无法失控的状态。只有当吸收的太阳辐射增加到峰值的最大OLR (328 W/m2)时,失控才变得不可避免。为了便于将来使用,我们将注意到,g = 10m/s2和1 bar N2的计算在Tg = 325K时,峰值OLR为310W/m2,而重力相同和3 bar N2的情况同样在310W/m2处有一个峰值,但峰值的位置移到了360K。金星表面重力略低的相应参数与这些数字相差不大。 Both cases asymptote to the OLR for pure water vapor when the temperature is made much larger than the temperature at which the peak OLR occurs.
•地球上失控的温室:目前吸收的太阳辐射(根据净云效应调整)为265 W/m2,地球目前处于地球引力行星的Kombayashi- Ingersoll极限以下。根据式1.1,为太阳光度继续增加,地球将超过291瓦/平方米的阈值,在大约7亿年内,失控成为可能。在17亿年后,它将超过310W/m2的阈值,在这个阈值中,大气中只有1巴的N2,除了水蒸气之外没有温室气体,失控是不可避免的。
•金星:金星目前的高反照率是由于硫酸云造成的,几乎可以肯定,在未来一段时间内,硫酸云就会消失干燥的空气.如果我们假设类似地球的反照率为30%,那么在太阳系历史的早期,金星吸收的太阳辐射将是327 W/m2。假设大气中有一两个大气压的氮气,除了水蒸气之外没有其他温室气体,这只是刚刚超过了金星表面重力的强制性失控阈值310W/m2。因此,可能被忽视的影响(云、饱和度低、a高反照率表面)可以让金星在一段时间内处于一种热的、蒸汽的、但不会失控的状态,有一个液体海洋。高层大气的高水蒸气含量仍然会使水的光解离和逃逸到太空的速度加快。然而,如果金星确实从海洋开始生命,它最终屈服于失控状态是合理的,因为以目前的太阳常数,没有硫酸云的吸收太阳辐射将是457W/m2,远远超过了失控的阈值。
•Gliese 581c:我们现在可以改进我们对太阳系外行星Gliese 581c的条件的早期估计,假设它的表面是岩石,它吸收的太阳辐射为583 W/m2。这一通量远高于334W/m2的阈值,即使考虑到大气中有2巴的氮气,对于一个引力是地球表面引力两倍的行星来说,这也是强制性的失控。因此,如果格利泽581c曾经有过海洋,它很可能已经进入失控状态;如果这颗行星的组成中包含了大量的碳酸盐,那么随后的气体排出很可能将它变成了一颗类似金星的行星。然而,仍需评估增加的经费所涉问题大气吸收由于m矮星主星的红外输出比例较大。
•类地轨道上冰卫星的蒸发:有人认为,如果木卫二或土卫六这样的冰卫星所在的轨道暗示着类地太阳辐射,那么它们可能成为宜居行星。然而,低表面重力的天体的低Kombayashi-Ingersoll极限严重限制了这种可能性。与冰的反照率在美国,这样的天体可以像雪球一样存在于类地轨道上,但如果表面解冻,或者一开始就没有冻结,那么与20%的反照率相对应的吸收的太阳辐射将是274W/m2,远远高于表面重力为1 m/s2的天体的232 W/m2的失控阈值。因此,在类地轨道上运行的小型冰冻卫星很可能蒸发掉,除非它们被锁定在雪球状态。
•撞击后蒸汽大气的寿命:假设在早期轰击后期,足够多的小行星和彗星撞击地球,蒸发了10巴的海洋,给地球一个10巴的大气,主要由纯水蒸气组成(根据研究,表面温度超过440K克劳修斯——克拉珀龙方程).蒸汽大气下完雨,温度恢复正常需要多长时间?为了解决这个问题,我们假设大气在冷却时保持饱和状态,并以地球的Kombayashi-Ingersoll极限所给出的最大速率损失热量;我们还需要从热损失中减去吸收的太阳辐射。对于早期的地球条件,净热量损失约为100W/m2。另一方面,在表面压力为ps的蒸汽大气中,地球表面每平方米的潜热为Lps/g,在规定的大气中为2.5•1011 J/m2。以100W/m2的速率去除这些能量需要2.5•109秒,即80年。在此期间,降雨率将是温暖但温和的:3.5(kg/m2)/天,或仅3.5毫米/天水的密度1000公斤/立方米。这是受辐射冷却速率限制的平均降雨速率,但在某些地方,由于风暴和其他大尺度大气环流的抬升和凝结,局部降雨速率可能会大几个数量级。
•岩浆海洋的冻结时间:在第一章中,我们介绍了早期地球上岩浆海洋的冻结时间问题,并在问题??中假设大气透明,估计了冻结时间。如果地球上的水足够丰富,那么岩浆海洋需要多长时间才能冻结大气由本质上是饱和的纯水蒸汽?时间的估计方法与问题??除了热损失率再次被认为是Kombayashi-Ingersoll极限(给出最大OLR)和太阳能吸收率之间的差值。对于早期地球来说,这将是大约100W/m2,这远远小于透明大气的情况,在透明大气中,基于 后两种估计遵循了斯坦福大学(Stanford)的诺曼•斯旺(Norman Sleep)提出的思路 再一次说明了“伟大的想法来自简单的模型”的原则。 假设火星每单位表面积吸收90W/m2的太阳辐射,估计撞击后火星上纯水蒸气大气的寿命。估计降水率,以毫米液态水每天。 P4 J 图4.39:不凝结温室气体对OLR曲线形状的定性影响。上面的曲线给出了由饱和可冷凝温室气体和非冷凝透明背景气体的混合物组成的大气的OLR,如图4.38所示的N2/H2O情况,而下面的曲线说明了如果添加大量不可冷凝温室气体,这种行为将如何发生。中间曲线给出了单组分饱和温室气体大气的OLR,如图4.37所示。 图4.39:不凝结温室气体对OLR曲线形状的定性影响。上面的曲线给出了由饱和可冷凝温室气体和非冷凝透明背景气体的混合物组成的大气的OLR,如图4.38所示的N2/H2O情况,而下面的曲线说明了如果添加大量不可冷凝温室气体,这种行为将如何发生。中间曲线给出了单组分饱和温室气体大气的OLR,如图4.37所示。 上述结果假定大气中存在的温室气体只有饱和的、可冷凝的温室气体。如果大气中也含有一种不凝结的温室气体,其总质量随着表面温度的升高而保持固定,会发生什么?例如,对于类地球或类金星的条件,人们通常需要考虑由饱和的可冷凝水蒸气、不凝结的二氧化碳和可能是透明的不凝结背景气体(如N2)的混合物组成的大气。在这种情况下,当水蒸气本身不能支持温室失控时,二氧化碳的加入能引发温室失控吗?我们将不追求这类详细的辐射计算,但一些简单的定性推理,总结在图4.39的草图,足以描绘出一般的行为。最基本的观点是,在足够高的温度下,大气完全由可冷凝成分主导,其质量随温度呈指数增长。因此,Kombayashi-Ingersoll极限将不受添加不凝性温室气体的影响。然而,随着越来越多的不凝性温室气体被添加到大气中,人们必须达到越来越高的温度才能接近极限极限温度r。在较低的温度下,大量非冷凝温室气体的加入使OLR降低到Kombayashi-Ingersoll极限以下。这是否会引发失控取决于情况的细节。 If the OLR curve without the noncondensible greenhouse gas is essentially monotonic in temperature, as in the one-component cases in Fig. 4.37, then the addition of the noncondensible greenhouse gas warms the planet, but does not trigger a runaway if the absorbed solar radiation is below the Kombayashi-Ingersoll limit. However, in a case like Fig 4.38, in which the OLR curve overshoots the limit and has a maximum, the addition of the noncondensible can eliminate the hump in the curve, eliminating the stable non-runaway state and forcing the system into a runaway. In the sketch, this situation is illustrated by the absorbed solar radiation line labeled "A". In that case, the addition of the noncondensing gas can indeed force the system into a runaway state. On the other hand, if the absorbed solar radiation is below the Kombayashi-Ingersoll limit, as in the line labeled "B", then the addition of the noncondensible greenhouse gas warms the equilibrium but does not trigger a runaway. 失控温室和Kombayashi-Ingersoll极限的概念可以推广到水蒸气以外的气体。例如,假设一颗行星表面有一个凝结的二氧化碳储层,根据行星的温度,它可能会以二氧化碳冰川或二氧化碳海洋的形式出现。具体而言,当地表温度高于216.5K时,可冷凝储层以CO2海洋的形式存在;否则它会以干-的形式出现冰冰川.如果大气处于平衡状态表面水库并且其中除了从表面蒸发的CO2之外没有其他气体,则可以使用单组分绝热和自制辐射代码来计算饱和CO2大气的OLR曲线,其结果类似于图4.37所示的水蒸气结果。不同表面重力下的结果如图4.40所示。总的行为与我们看到的水蒸气非常相似,但整个系统在较低的温度下运行,并且OLR在比水蒸气低得多的温度下达到极限值。 二氧化碳失控对现在和过去的二氧化碳在火星上可能存在的形式施加了一些有趣的限制。对于火星表面重力,CO2的Kombayashi-Ingersoll极限略高于63W/m2。因此,当吸收的太阳辐射超过这个值时,地球表面就不可能存在一个凝结的二氧化碳的永久储存库;它会升华或蒸发到大气中,并继续使地球变暖,直到所有的冷凝储层都转化为气相。目前,全球平均太阳能吸收大约是110瓦/平方米,所以地球远远高于二氧化碳的失控阈值。由此我们可以得出这样的结论:火星上不可能有一个可观的、可以与大气交换的冷凝二氧化碳的永久储存库。然而,请注意,这并不排除二氧化碳雪在地表的临时积聚。这种沉积物可以在冬季两极附近形成,但在春季临近时又升华回大气中。这种情况可以认为是由于冬季极点附近的局部吸收的太阳辐射低于CO2的Kombayashi-Ingersoll极限。当地的推理适用,因为目前火星稀薄的大气层不能有效地从夏季半球输送热量。 即使没有厚厚的二氧化碳大气层的反照率,早期火星吸收的太阳辐射也只有77W/m2。对于纯二氧化碳大气来说,这仍然略高于Kombayashi-Ingersoll极限,但考虑到大气的散射效应,也许还考虑到大气中氮的影响,早期火星很可能有持续的永久性二氧化碳冰川,前提是有足够的二氧化碳供应。因为地球是如此接近一个阈值,一个更详细的计算-可能涉及到考虑大气的热量运输-将需要解决这个问题。 类似地,可以使用第4.4.8节中描述的连续介质吸收特性计算甲烷的Kombayashi-Ingersoll极限。这一计算将决定一个天体表面是否有永久的甲烷海洋、沼泽或冰川。 任何气体在足够低的温度或高压下都是可凝结的,事实上,正是Kombayashi-Ingersoll极限决定了从地球内部释放出来的挥发性温室气体是在大气中积聚,还是积聚成一个巨大的冷凝储层(可能是冰川或海洋)8。在后一种情况下,额外的放气进入冷凝储层,而大气中以气相保留的挥发性物质的数量由行星的温度决定。只有当吸收的太阳辐射低于有关气体的Kombayashi-Ingersoll极限时,冷凝的储层才能形成,即使如此,也只有当可用挥发物的总质量足以使大气达到饱和状态时才能形成。作为后一种约束的一个例子,让我们假设火星在一个 没有气体的大气还可以去别的地方;水可以进入矿物质的水合作用,二氧化碳可以被结合在一起碳酸盐岩. 表面压力(巴) 表面压力(巴) 表面温度(K) 图4.40:饱和纯CO2大气的OLR与表面温度的关系。计算是根据每条曲线上的地表重力值进行的。顶部的刻度给出了与较低刻度的温度相对应的表面压力。 表面温度(K) 图4.40:饱和纯CO2大气的OLR与表面温度的关系。计算是根据每条曲线上的地表重力值进行的。顶部的刻度给出了与较低刻度的温度相对应的表面压力。 更遥远的轨道,吸收的太阳辐射只有40W/m2。则由图4.40可知,饱和时平衡表面温度为165K,对应的表面压力为5600 Pa。为了达到这个表面压力,需要每克排放5600个气体,或每平方米地球表面排放1509公斤二氧化碳。在地球上,由于地球低于Kombayashi-Ingersoll水蒸汽极限,因此排出的水蒸气会积聚在海洋中。以目前的太阳亮度来看,金星(没有云)远远超过了极限,所以任何蒸发的水蒸气都会积聚在大气中(除了泄漏到太空)。对于二氧化碳来说,地球、火星和金星都超过了Kombayashi-Ingersoll极限,所以排出气体的二氧化碳会在大气中积累(除了以矿物形式结合的二氧化碳)。即使你拿走了让二氧化碳以碳酸盐形式结合的水,地球也不会形成二氧化碳海洋;它将成为热的金星而是像行星一样,拥有稠密的二氧化碳大气。 在结束之前,我们必须提到我们对失控温室现象的讨论的两个严重局限性。首先,在计算Kombayashi-Ingersoll极限时,假定大气中充满了可冷凝的温室气体。然而,真实的大气可能在很大程度上是欠饱和的,尽管决定欠饱和程度的动力学是复杂的,很难在简化模型中捕捉到。饱和不足可能会提高触发失控状态所需的太阳辐射阈值。第二个限制是计算是在晴朗的天空条件下进行的。云通过短波反照率施加冷却影响,通过对OLR的影响施加变暖影响,这种平衡也很难通过任何理想化的计算来确定。云层是否对失控的温室气体有抑制作用是众多遗留的大问题之一。 继续阅读:真实气体环境的纯辐射平衡 这篇文章有用吗?
表面温度
