Pq Pq Pq Ps Pq Ps cosZ Pqqs Pqqs Pqqs
我们去掉第一项,假设行星的半径是它到太阳距离的一小部分。出于同样的原因,分母中的\QS\可以很好地近似地替换为\PS\,使表达式以两个单位向量之间点积的形式表示。设n1 = PQ/\PQ\, n2 = PS/\PS\,单位向量在局部笛卡尔坐标系中有如下分量。
n1 = (cos($)因为(h),因为($)罪(h), sin ($)), n2 = (cos (5), 0, sin (5)) (7.6)
where cos(Z) = cos($) cos(5) cos(h) + sin($) sin(5)(7.7)当cos Z < 0时,太阳在地平线以下。
天顶角的余弦值在h = 0时达到最大值cos($ - 5),在h =±n时达到最小值- cos($ + 5)。当\$\ > \n/2 - 5\时,这两个值都在地平线以上,对应于永恒的极地夏日。当\$\ > \n/2 + 5\时,这两个值都在地平线以下,对应的是永恒的极地冬夜。在冬至时,5的极值为±7。因此,在向极地n/2 - 7纬度的地区,一年中的某些时候会经历永久的白天或黑夜。这些圆被称为南极圈和北极圈究竟除了永恒的白天和黑夜之外,还有一条明暗分界线将地球上光明的一面和黑暗的一面分开。终止符的位置由cos ht = - tan($) tan(5)(7.8)给出。
如果^是行星旋转的角速度,那么行星的一天为Tday = 2n/il个时间单位,则日光的时间单位数为2ht/Q = (ht/n)Tday。对于永恒的夜晚,我们采用惯例ht = 0,对于永恒的白天,我们采用惯例ht =±n。
习题7.3.2对于给定的纬度0,日照最少的小时数是多少?哪一天白天的时间最长?地球现在的倾斜度是23.5度日长23.94小时。画一张地球上白昼时间的最大值和最小值与纬度的关系图。
天顶角的昼夜变化导致白天热,夜晚冷。这里的热响应时间足够长,可以平均出可观的部分白天的温度日平均入射太阳通量是一个有信息量的统计量。由于每平方米表面的入射太阳通量为L cos Z,其中L是太阳常数W/m2,可以通过在行星旋转周期内平均cos Z来获得日平均太阳通量。这就产生了一个无量纲的通量因子f,用它乘以太阳常数就可以得到日平均值太阳辐射事件在地球球面的每一平方米上。日平均值可以进行分析,得到
= - [cos(^) cos(5) sin(ht) + sin(^) sin(5)ht] n其中ht由公式7.8决定。这种日平均值的推导假设一天的长度远小于一年的长度,因此5在一天的过程中可以被视为常数。如果一天的长度在一年的长度中占很大一部分,就像水星或金星这样几乎被潮汐锁定的行星一样,这个表达式仍然会给出沿着纬度圈的正确平均值,但这个平均值不再与一天的时间平均值相同。
在二分点期间,5 = 0,f = cos(^)/n,与倾角无关。这与我们先前用直接几何推理得到的结果是一致的。在一年中的其他时间,日平均通量受两个相互竞争的因素支配:不同的白昼长度,这往往在夏季极点附近产生较高的通量;平均天顶角,这往往在太阳下纬度附近产生较高的通量(如果倾角不是太大,则仍在赤道附近)。日平均日照最大值出现的纬度总是在次太阳纬度5和夏极之间。当5 = 0时,最大值出现在赤道,一个小的数值实验表明,当5 = 23.4o时,最大值的纬度增加到大约43.4o(类似地,在南半球,随着符号的反转)。对于更大的5,在极点上,白昼长度的影响超过了倾斜角度的影响,最大的影响发生在夏季极点本身。目前,这种状态只会在冬至发生地球的倾角和火星;因此,在这两种情况下,夏半球至日日照是相当均匀的。同样值得注意的是,当|5| > 17.86o时,夏季极点的日平均日照超过赤道的日平均日照。
要对季节周期有一个大致的了解,请回忆在季节周期中5从-7变化南半球夏季夏至:北半球夏至至点至7点,在两个至点之间的春分点处值为零考虑一个具有均匀反照率的行星,这样吸收的太阳辐射是由分布决定的吗入射太阳辐射.进一步假设热响应时间足够长,足以平均出日周期,但与一年的长度相比较短。如果倾角低于23.4度,“热点”在南半球开始向赤道偏极一段距离,随着春分的临近向赤道移动,然后在北方夏至临近时向北半球移动类似的距离。如果倾角大于23.4o,热点从南极开始,在季节的这个点间断地跳跃到-43.4o
秋天
秋天
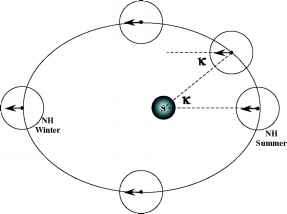
春天
图7.4:
春天
图7.4:
当次太阳纬度接近23.4o时,它会平稳地穿过赤道,到达43.4o,然后不连续地跳跃到北极。请注意,在这两种情况下,热点每年在春分穿过赤道两次;两个至日是赤道最冷的时候。赤道的气raybet雷竞技最新候有一个周期性,相当于半个地球的周期。
它只需要把5表示成行星在轨道上位置的函数。行星像陀螺一样旋转,如果没有力矩作用在行星上(我们稍后会放松这个假设),它的角动量是守恒的。因此,旋转轴全年相对于遥远的恒星保持固定的方向。这就是北极星一年四季都是北半球北极星的原因。设k为描述行星位置的角度,如图7.4所示。我们将采用k = 0发生在北半球夏至的惯例。我们将k称为季节角,但它更常见(也更模糊)地被称为太阳的经度。在我们的例子中,我们已经定义了相对于北半球夏至的太阳经度,但其他选择也很常见,例如相对于北方冬至或春分定义它。在讨论地球以外的行星上的季节周期时,季节角度几乎普遍用于描述行星在其周期中的位置,因为这种描述避免了为每个行星命名月份的需要。如果我们将旋转轴投射到黄道平面上(即包含行星轨道的平面),那么这个矢量与PS的夹角等于k。投射到黄道平面上的旋转轴就像时钟的指针,每年绕着钟面旋转一次,尽管如果轨道不是完美的圆形,其速度就不均匀。
设n为黄道平面的单位法向量,na为旋转轴方向的单位向量。引入一个新的笛卡尔坐标系x指向PS, z指向n, y以右手的方式垂直于这两个坐标。那么na = (cos(k) sin(Y), sin(k) sin(Y), cos(Y))太阳的纬度是na与x轴夹角的补角,从中
继续阅读:热惰性
这篇文章有用吗?