分子散射瑞利散射

瑞利散射理论是一个经典的(即非量子)电磁散射理论，它开始作为一个理论的电磁平面波散射从一个小球体与实折射率n。“小”在这里是指与散射光的波长相比小。在瑞利极限下，粒子的散射计算非常简单，因为入射电场在粒子上几乎是恒定的，这使得计算诱导散射非常简单电磁场在粒子内部。本质上，入射波的电场导致粒子内的电荷迁移，使正电荷积聚在一侧，负电荷积聚在另一侧，导致偶极矩以与入射波相同的频率振荡。折射率实际上是测量介质极化率的一种方法，即电场强度与诱发偶极矩强度之间的比例关系。瑞利极限中的散射波就是电磁辐射由振荡偶极子发射，这是电磁理论中最基本的计算之一。

也许令人惊讶的是，瑞利理论很好地描述了来自分子的光散射，即使分子不是电介质球体。确实，典型的尺寸

0.01

o 0.0001

0.01

o 0.0001

-n_i水冰

1000

-n_i水冰

1000

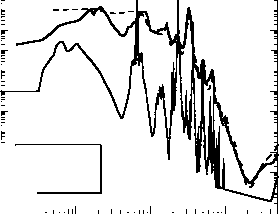
图5.4:液态水、水冰和二氧化碳冰的假想折射率。

分子的波长(例如氮气的波长为0003 pm)比可见光甚至紫外线的波长小得多，但人们可能会认为分子的量子响应可能会在本质上影响散射。当然，瑞利理论并没有为计算提供一个合适的基础分子吸收正如我们在第四章中所看到的，辐射与分子的量子性质有着千丝万缕的联系。我们不打算进一步解释为什么经典理论对分子散射比对分子吸收更有效，但这确实是一种方便的转变。在实际应用中，使用光谱测量的吸收系数来计算气体吸收，同时使用瑞利散射来计算气体散射，效果很好。

对于球对称散射体，瑞利理论给出了散射截面的公式:

A是波长入射光在真空中，ap为散射体的极化常数，它表示电场与诱导偶极矩之间的比例关系。在实践中，偏振常数是从散射截面本身的测量中推断出来的。它只是波长的弱函数。瑞利散射截面与波长有很强的相关性;短波(高波数)散射比短波强得多长波浪(低波数)。对地球蓝天的解释可能是瑞利散射最著名的应用:蓝色穿过紫光更短的波长比其他可见光谱要高，因此在空气分子散射太阳光束引起的漫射辐射中占主导地位。对于非球对称的散射体——包括我们所考虑的大多数大气中存在的所有多原子分子，如N2、H2和CO2——偶极矩与施加的电场方向不同，这种效应略微改变了散射截面的表达式。气体中的分子是随机取向的，可以表明，对所有取向平均后，修正后的横截面由式5.24中的对称横截面乘以

	H2	他	空气	N2	O2	二氧化碳	水	NH3	甲烷
Xsca	1.	.0641	4.4459	4.6035	3.8634	10.5611	3.3690	7.3427	10.1509
Xsca / m	1.	0.0321	0.3066	0.3288	0.2415	0.4800	0.3743	0.8638	1.2689
托盘	0.40653	0.01305	0.12464	0.13367	0.09818	0.19513	0.15216	0.35116	0.51585
表5.2:	瑞利散射		横截面，以及		每个截面		单位质量,	相对	H2。

这些结果是根据折射率的观测得出的，没有考虑到偏振因素的变化。H2在波长为10 ^m时的散射截面和单位质量截面分别为1.4•10-38m2(4.215•10-12m2/kg)、8.270•10-33m2(2.490•10-6m2/kg)和3.704•10-28m2(。11 m2/kg)，波长为。1 yU,m。托盘是由于瑞利散射在1 ^m的1巴大气下的指示气体在地球重力下的光学深度。

除以3(2 + S)/(6 - 7S)，其中S是去极化因子，这是分子的性质。对于球对称散射体，去极化因子为零。就我们的目的而言，去极化因子的影响不是很重要。O2为0.054,N2为0.0305,CO2为0.0805。这些只导致散射截面的微小增加。

利用麦克斯韦方程，还可以通过n = 1 + 2nNap(5.25)的关系推断折射率与组成介质的分子的极化率有关。

N是单位体积的分子数。这是一个非常有用的关系，因为它允许人们通过简单的测量来确定瑞利散射截面折射率，这可以通过直接测量光从透明固体容器(例如玻璃)进入气体时的偏转角来实现。

表5.2给出了一些常见大气气体相对于H2的实测瑞利散射截面，以及相应的单位质量截面。在标题中给出了一些波长的H2横截面的绝对值，允许其他分子的实际横截面易于计算;由于折射率对波长有轻微的依赖性，标题中给出的H2值与1/A4波长缩放略有偏差，但一般来说，使用四次方定律推断其他波长是足够的。他是一个特别弱的分散者。其余大部分分子的单位质量散射截面都比H2略小，只有CH4略大。

为了了解散射是在各种情况下，我们可以使用单位质量的横截面来确定大气整个柱的光学深度。当光学深度较小时，大气几乎不散射，而当光学深度较大时，大量辐射被散射;在的情况下入射太阳辐射，这意味着大量入射光束将被反射回太空。表5.2的最后一行给出了在地球重力下由1巴给定气体组成的大气的光学深度。我们可以把这个比例扩大到其他行星，方法是乘以适当的表面压力，再除以行星相对于地球引力的引力。光学深度值在波长2 ^m，在可见光谱的中心，这也是附近的峰值太阳光谱．对于地球目前的大气层，光学深度很小，但并非微不足道;瑞利散射影响入射光束的12%。早期火星的大气中有2巴的二氧化碳，瑞利散射是相当强的，这是由于二氧化碳相对于空气的散射截面有所升高，重力较低，以及额外的表面压力。早期火星的瑞利光学深度是可见的1.03。太阳辐射的相关反射是早期火星变暖的一个重要障碍，会产生气态CO2温室效应。如果把金星上的反射云拿走，二氧化碳的瑞利散射仍然会使金星具有相当的反射性，因为金星上90巴二氧化碳大气的光学深度接近20巴。在没有云的情况下，土卫六上1.5巴的N2大气的光学深度为1.45。木星前10个主要由H2组成的大气柱的光学深度为1.6，同样也有显著的散射。

其他波长的光学深度可通过按1/A4缩放这些结果得到。因此,在热红外波长比我们所考虑的波长大5倍或更多，光学深度至少小625倍;瑞利散射在这些波长上是不显著的，这就是为什么在计算OLR时忽略气体散射是安全的。另一方面，瑞利散射光学深度至少是紫外线的16倍。我们将学习如何将这些光学深度值转换为行星地表反射率第5.6节。

瑞利散射不是各向同性的，但相位函数在正反向之间是对称的。在双流近似中，我们实际上不需要散射截面以外的任何信息。无论如何，看一下相函数是值得的，如果只是为了了解它有多接近各向同性。给定去极化因子8，瑞利相位函数为

P(cos©)= 2^(1 + 8 +(1 - 8)cos2©)(5.26)

由此可见，瑞利散射具有轻微的各向异性，前后方向的散射比垂直于入射光束方向的散射强。对于8 = 0，正向和反向方向的散射强度(©= 0,n)是侧面叶(©= n/2)的两倍。增加8可以减小各向异性。事实上，实验室测量侧散射和正向散射的强度提供了一种估计去极化因子的方便方法。

继续阅读:带散射的两流方程

这篇文章有用吗?

0 0