一些基本轨道力学

艾萨克·牛顿爵士指出，一颗行星围绕其恒星旋转的轨道呈椭圆的形式，椭圆的焦点位于系统的质心。由于恒星的质量通常比它们的行星大得多，所以质量中心在大多数情况下与恒星的中心是相同的。轨道的椭圆性质对季节周期有重要的影响，因为行星在一年中的某些时候比其他时候离太阳更远。这使得太阳“常数”L是一年中的时间的函数。在地球上，我们不会太注意到这种影响，因为我们的轨道几乎是圆形的。尽管如此，这种效应对气候的长期演变具有重要影响。raybet雷竞技最新在其他星球上，它甚至更重要。

一颗行星最接近它的恒星的距离称为近日点，我们称之为rp。最遥远的距离叫做距离远日点半长轴为a = (rp + rap)/2。设«为恒星与行星之间的直线所形成的角度，定义为«在近日点处= 0。在极坐标下，椭圆轨道的方程为

其中e为轨道的偏心率，在区间[0,1]内。E = 0产生圆形轨道，而椭圆在E ^ 1时逐渐变长。具体来说，近日点为(1 - e)a，远日点为(1 + e)a，远日点距离与近日点距离的比值为(1 + e)/(1 - e)。为了得到半小轴，我们最大化r(K1)s«n(K1)，得到a\/1 - e2。因此，小轴与长轴的比值为%/1 - e2。轨道的几何形状如图7.10所示。

什么样的离心率会产生一个轴比为3:1的椭圆?画出这样一个图

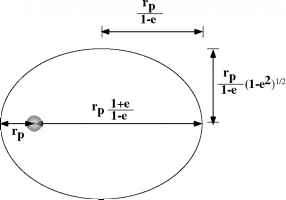
图7.10:偏心率e = .66的椭圆轨道几何图

椭圆，表示太阳相对于轨道的正确位置。

的变化太阳常数是然后由

其中木卫一是恒星的输出功率(例如，目前太阳的功率约为3.8x1026瓦)。每年与太阳距离的变化导致了“距离季节”，这在半球之间是同步的。这与“倾斜季节”(地球和火星的主导)形成对比，这两个半球之间的相位不一致，一个半球享受冬天，而另一个半球则遭受炎热的夏天。在小偏心极限下，远日点太阳常数与近日点太阳常数之比为1 + 4e。这代表了一个非常大的变化，即使是适度的偏心。就目前而言地球的偏心率(.017)，即近日点与远日点太阳常数相差93W/m2，为6.8%。为了将这一通量转化为粗略的温度估计，我们将4除以地球表面的平均值，并应用典型的地球OLR(T)斜率2W/(m2K)，得出近日点和远日点之间的温差超过11K。这代表了距离季节的振幅。对于火星来说，其目前的离心率为0.093，这种影响甚至更大。近日点到远日点的通量变化为37%，即219W/m2。在火星的条件下，大气的温室效应很弱，这转化为30K的振幅。

为了确定r的时变关系，我们必须知道Ki(t)。因为轨道不再是圆形的，角速度不再是恒定的;行星靠近太阳时比远离太阳时移动得快。轨道位置随时间的变化没有解析表达式。然而，它可以很容易地通过数值求解一阶微分方程来计算，这个方程可以从开普勒等面积定律推导出来，也可以直接从角动量守恒推导出来。我们将走后一条路。设v±为速度垂直于行星与恒星连接线的分量。由角动量守恒，rv±= J与时间无关。然而，轨道的角速度仅仅是v±/r，因此角度满足方程dKi = J = J (1 + ecos(Ki))2

Dt r2 a2 (1 - e2)2 ()

这个方程表明，行星的角速度在接近近日点时加快，在接近远日点时减慢。因此，行星靠近太阳的时间比距离更远的时间要短，“夏天的距离”比“冬天的距离”短。

一年中太阳常数的平均值可以写成

1 Io a2 a2。

< L >= -2 < ^ >= La <> (7.28)

其中尖括号表示行星一年的平均值，La是在等于轨道半长轴距离处计算的太阳常数。我们可以利用Eqn. 7.27中出现的相同的1/r2因子来将平均太阳常数与行星一年的非量纲化持续时间联系起来。具体来说，将Eqn. 7.27对一年进行积分，并除以年长的结果

Ty，其中t* = Ty/(2na2/J)， Ty是一年的维度长度。2na2/J是半径为a的圆形轨道的年长。Eqn. 7.27的数值积分表明，以这种方式定义的无量纲年随着轨道偏心程度的增加而减少。当e = .1时，t*为.995，当e = .25时，t*为.968，当e = .5时，t*为.866。

大多数行星的轨道接近圆形;除去水星和冥王星，其他行星目前的偏心率在0.07到0.093之间。即使是冥王星，最古怪的行星，也只有。244。注意，近日点和远日点距离的差值是O(e)，而长轴和小轴的比值仅偏离单位O(e2)。因此，对于小e，轨道看起来仍然像一个圆，但太阳从圆的中心偏移了O(e)。对于小e, Eqn. 7.27可通过e中直接展开近似求解

Ki(t) = J [t + eF(t) + e2G(t)] (7.30)

在e中匹配类似项，得到解k1 = 2nt* +2ecos2nt* + e2 [nt* + y sin4nt*] + O(e3) (7.31)

其中t* = tJ/(2na2)。一阶项在一年中引起轨道角速度的O(e)变化，但这一项本身并不改变一年的长度。考虑到二阶项，可以推断出年的无维长度约为t* = 1 - e2/2。因此，与半径等于半长轴的圆形轨道相比，年平均日照变化很小。对于e = .1，接近火星的现值，离心率仅使平均日照增加0.5%。对于e = 0.02，与目前的地球相似，增加的是微弱的0.02%，或0.274 w /m2。除非在非常特殊的情况下，轨道偏心率通过季节周期的中介影响气raybet雷竞技最新候，而不是通过对年平均辐射预算的任何影响。

轨道偏心率对行星气候的影响源于季节与行星距离的相互作用raybet雷竞技最新倾斜季节。这些季节中的每一种都有一个行星年的周期，所以相互作用的性质是由北半球夏至发生的轨道位置决定的，相对于近日点的位置测量。这可以通过一个角度来测量，称为进动角或进动相位。我们将定义相位，当它为零时，北半球至点发生在近日点。也通常定义为近日点和北半球春分(“春分”)之间的角度。当岁差角为零时，距离季节使北半球的季节周期更强，因为当行星离太阳最近时发生“北倾夏”，而当行星离太阳较远时发生“北倾冬”。相反，当进动角为零时，南半球的季节周期减弱。当进动角为180°时，半球之间的情况正好相反，南半球变得非常炎热的夏季和非常寒冷的冬天而北半球则经历了更为温和的季节。当进动角为90°或270°时，冬至条件不再受距离季节的影响，而是春分比秋分变暖，反之亦然。

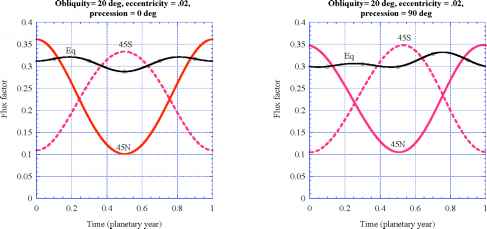
图7.11说明了偏心率和岁差对日照季节周期的影响。这些结果是通过数值求解式7.27，并将K1(t)代入式7.10和式7.9给出的通量分布函数中，将其相移以考虑进动角。已知K1(t)我们也知道r(t)利用这一点，我们将通量因子乘以(a/r(t))2来解释轨道距离的变化。这是图7.11中选定纬度处绘制的数量。将此通量因子乘以距离等于半长轴的太阳常数，以获得以W/m2为单位的实际日照。利用Eqn. 7.9的对称性，通过简单地平移半年所示曲线，并互换两个半球，可以得到180o和270o进动角的结果，因此不需要单独讨论这些情况。

对于这两种偏心率，我们看到，当进动角为0o时，北半球的热带外季节周期变得更加极端，而南半球的季节周期则有所缓和。在赤道，两个平分点的日照相同，但赤道日照最大的时间移向北方夏至，在这种情况下，这也是近日点的时间。对于较大的类火星的偏心率(e = .1)，赤道最大日照实际上发生在至日。在90度斜度的情况下，两个半球的温带季节周期强度相同，但现在的秋分条件彼此不同，秋分受到的日照比春分少。此外，最大和最小热带日晒的时间也显著地偏移于圆形轨道的时间。轨道速度变化对季节周期的影响对于较低的，类地球的，离心率来说几乎是可见的，但是对于较高的离心率情况来说是显著的。0°岁差时，南半球夏季长于冬季，北半球冬季长于夏季;对于90度岁差，每个季节的日晒增加率和季节结束后的日晒减少率之间存在明显的不对称。例如，在北半球，夏天很快到来，但向冬天的过渡却需要很长时间。事实上北半球，南半球赤道日照最大值都在大约四分之一年内聚集起来，这表明距离季节开始主导倾斜季节，即使在这种适度的偏心率下。岁差相位对各纬度年平均日照的影响不显著;对于图7.11所示的高偏心和低偏心情况，改变进动相位使年平均通量因子保持不变，至少保持小数点后四位。

注意，当离心率较大时，旋进角对气候的影响较大，而当离心率为零时，旋进角对气候的影响较小。raybet雷竞技最新的进动效应角度离心率和轨道离心率是相互关联的，不能被解开。

目前,地球的旋进这个角度接近180度，因此南半球被驱使走向更热的夏天和更冷的冬天，而北半球则被驱使走向一个更弱的季节周期。这种模式在观测中没有表现出来(图7.2)，因为北半球比南半球有更多的土地，使其具有更强的季节性

倾角= 20度，偏心率= 1，进动= 0度

	情商	45岁
/			N	＼
y		\•

倾角= 20度，离心率= 1，进动= 90度

		* I /✓	＼
	v * X *		我\	1
y '	# x。* x ^	45 n	% - - - - - -

图7.11:在赤道、北纬45度和南纬45度，倾角为20度的行星的太阳通量因子的季节周期。为了得到一年中任何给定时间的日照量，这个通量因子乘以近日点时的太阳常数。结果显示，类地球的偏心率为0.02(上一行)，类火星的偏心率为0.1(下一行)。左列给出了a的结果岁差的而右边给出的结果是90度，两者都是相对于北半球夏至测量的。

周期，因其较低热惰性．不过，相对而言，北半球的季节周期比进动角为90度或0度时要弱。巧合的是，目前火星的进动角也在180度左右，因此南半球火星的冬天预计会比北半球冷得多。这种情况确实发生的证据，以及它对火星气候更广泛的影响，将在第7.7节中讨论。raybet雷竞技最新

地球和火星的进动角和轨道偏心率在过去是不同的，将来也会不同。这对气候的演变有一些极其重要的影响，我们现在将注意力转向气候的演变。raybet雷竞技最新

继续阅读:米兰科维奇在火星上骑车

这篇文章有用吗?

0 0