平均自由程

分子在气体中碰撞前运动的平均距离称为平均自由程。为了得到平均自由程的估计，想象背景气体粒子是静止的。让我们的半径为r0的测试分子在上一小节中使用的固定点晶格中移动。我们的原型分子和背景分子的中心距离在2r0以内时会发生碰撞(图2.2)。我们可以认为测试分子的半径为2r0，晶格由静止点组成(见图2.3)。因此，当测试分子在晶格中移动时，它扫出一个半径为2r0的圆柱体。在时间上，扫出的体积为(2r0)2n * vAt(单位体积的数量乘以体积)。清扫器的截面积有时用符号ac表示，称为碰撞截面(见表2.2)。背景的数量

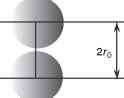
图2.2碰撞时刻两个球形分子的中心之间的距离为2r0。

图2.3分子移动距离vAt时，遇到长度为vAt，截面积为4nr2的圆柱体体积内的所有点中心。卷中点中心的数量为n04n r0 vAt。

该圆柱体中的分子中心为n0 × acvAt(单位体积上的分子数×圆柱体的体积)。则单位时间内的碰撞次数(碰撞频率)为fcoll = n0acv[碰撞频率]。

我们可以计算碰撞之间的平均距离为[单位时间距离]=[速度]x[碰撞之间的时间](最后一个因子是碰撞频率的倒数):

没有< 7 noCTc简历

[平均自由程，近似形式]。

希腊字母X在大多数文本中被用来表示平均自由路径。实际上，当所有的粒子都在运动时，这个问题是有可能解决的，推导可以在有关气体动力学理论的书籍中找到。同样的公式适用于平均自由路径，除了额外的因子V2 = 1.414…分母中:

V2no Oc

[平均自由路径，更精确的形式]。

表2.1 STP气体动力学理论中的一些特征长度(均以纳米为单位，10-9米)

波尔	分子间	的意思是	波长的
半径	间距	自由程	黄灯

0.053 3.3 52 500 .

0.053 3.3 52 500 .

表2.2 nm2中感兴趣气体的一些碰撞截面ac

对于物种间的估计，使用平均值。数据来自Atkins和de Paula(2002)。

Ar-Ar N2-N2 O2-O2 H2-H2

0.36 0.43 0.40 0.27

对于典型气体r0 = 2 × 10-10 m (0.2 nm)，因此ac = 4nr2 ~ 5 × 10-19 m2 (0.5 nm2)。使用上面的n0，我们得到X ~ 5.23 X 10-8m (52.3 nm)，这大约比STP的分子间距大一个数量级(表2.1)。

作为数密度垂直依赖关系的模型:

其中z为海拔高度，H为比例尺高度(中纬度地区通常为8公里，热带地区可达12公里)。我们的指数模型是虚构的，但它是一个很好的近似值。在z = 0 H 2H处，STP在z = 0处的典型平均自由路径是什么?答:

则:Xz=0 = 52 nm, Xz=H = 141 nm, Xz=2H = 384 nm。□

从前面的例子中，我们看到，平均自由路径与我们熟悉的日常大小的事物相比，尤其是天气现象，即使在几个比例尺的高度(很好地进入平流层)，仍然非常小。当气体体(比如风暴或冷气团)的尺寸比平均自由路径大时，我们可以忽略分子运动，将气体视为流体，遵循流体力学的宏观定律。在大气科学中，这种情况通常发生在海拔约100公里的高空。

平均自由路径还让我们了解了发生属性传输的长度尺度。如果一种性质是通过分子之间的碰撞来传输的，那么它必须发生在与平均自由程相当的长度尺度上。这样的过程被称为扩散过程，与对流等流体运动相比，它们是相当缓慢的。

2.1.3动力理论压力

理想气体压力的直观感觉可以通过将气体封闭在边长为L的立方盒中得到(见图2.4)。想象一下，一个分子从左到右穿过盒子，然后反弹到壁上。一个往返的时间是2L/v0，其中v0是分子的速度。在反射时，它经历动量变化a (m0v0) = 2m0v0。每个反射都对墙壁施加一个脉冲力(参见下面的物理更新)。这种反射的频率(整个盒子的分子)是如此之大，以至于力是有效稳定的(我们将在后面看到典型的分子速度是数百ms-1)。单个分子的这种脉冲速率是动量的变化除以反射之间的时间间隔，2m0v0/(2L/v0) = m0v^/L。如果我们假设三分之一的分子是左右移动的(其他的分子是上下进出的)，那么左右移动的分子数是noL3/3。作用在墙上的总力是

	V
	l

以速度v0从左向右运动的分子被壁弹性反射。碰撞后，速度是-v0。这个立方体的边长尺寸是L。

以速度v0从左向右运动的分子被壁弹性反射。碰撞后，速度是-v0。这个立方体的边长尺寸是L。

作用在壁上的总力也应该是压力乘以壁面面积，可以表示为

把这些式子等号

[与(2.8)有关的压力

其中超棒表示分子速度概率分布的统计平均，v0。因为我们知道理想气体的状态方程，p = n0kBT(从实验中)，我们可以用它和刚刚发现的关系来确定相应的系数，并得出新的关系:

[动能和开尔文温度]。(2.9)

注意，左边只是盒子里分子的平均动能(2m0v^)。这个关系式表明，用开尔文表示的温度与单个分子的平均动能成正比。比例系数因此被确定为2倍玻尔兹曼常数。注意，当绝对温度或开尔文温度T为零时，分子处于静止状态(v^ = 0)。在此温度下，所有热运动都假定为零，至少在我们定义的理想气体中是这样。实际上，在0 K时不存在理想气体(任何实际气体都会被液化或固化此外，量子力学告诉我们，即使在这个最低的低温下也有运动。幸运的是，我们在气象学中从来没有遇到过这种低温，理想气体定律实际上总是适用于我们感兴趣的气体。

虽然上面的推导被高度简化，省略了许多细节，如不垂直于壁的飞行，分子速度的分布，分子之间的碰撞等，这些细节在更严格的推导中抵消了。因此，公式及其解释是正确的。

物理复习:脉冲力当一个粒子从一个刚性表面反射时，它在表面上施加一个力。作用在壁上的力可以通过牛顿第二定律对碰撞时间的积分得到:

- 1f t+ t / 2dv (t) f t = - mo - dt

T Jt-r/ 2dt其中T是分子与壁接触的(很短的)时间间隔。不幸的是，我们不知道T的一般值。然而，在间隔(t - t/2, t + t/2)以外的较长时间内，被积体消失，因此积分周期可以从t - Trt/2延长到t + Trt/2，其中Trt是分子在与壁面碰撞之间往返的时间长度。在单个分子的往返行程中施加在壁上的力为

如果往返时间(Trt = 2L/v0)足够短(与缓慢的墙壁的响应时间相比)，墙壁将感受到这个量级的几乎稳定的力。现在如果我们把所有分子的碰撞相加，就像压强的推导一样，我们可以保证有一个垂直于壁面的稳定力。

还有一些未解决的问题必须解决。首先，并不是所有的分子都严格地在x, y和z方向上运动。这可以通过注意到对于垂直于x方向的墙壁，只有运动的x分量起作用来处理。y和z分量不影响这个壁。碰撞是否一个接一个地抵消了它们在与墙碰撞前后的y和z分量?毕竟，在分子水平上，壁不是光滑的表面。答案是，从长期来看，对许多粒子进行平均，这种抵消是完全的。最后，分子不会不间断地从盒子的一端移动到另一端。在它们与另一个分子碰撞之前，它们只走一条平均自由程(在STP下只有几十纳米)。这个问题的解决方法在于动量守恒。 After a collision the x component of momentum is conserved for the colliding pair and it is the momentum change at the wall that matters, whether it is the same molecule or not.

在气象学等特定应用中，将理想气体定律转化为另一种形式是有用的，即通过乘以和除以单个分子的质量m0:

其中p为kgm-3的质量密度(p = m0n0 = M/V)，由R定义的气体常数为kB/m0(注意:这不是后面定义的通用气体常数)。干燥空气

Rd = 287JK-1 kg-1。

注意，气体常数的定义取决于单个分子的质量m0。干燥空气是不同理想气体的混合物。Rd的值考虑了这种混合，稍后会解释。

表2.3干空气组成

	百分比
	按体积	百分比	分子
组成	(数量)	通过质量	重量
氮	78.09	75.51	28.02
氧气	20.95	23.14	32.00
氩	0.93	1.30	39.94
二氧化碳	- 0.03	~ 0.04	44.01

表2.3给出了由体积百分比组成的干燥空气-这是一种物质的数量密度n0与总数量密度的比率。同一表格还给出了质量百分比-样品中成分的质量与整个样品质量的比率(x 100)。

例2.3在270k和500hpa水平下，一团干燥空气的密度是多少?答案:用p = p/(Rd T):

例2.4在STP下，空气分子的均方根(rms)速度是多少?答案:我们会写字

例2.5“空气”在STP的碰撞频率是多少?(空气之所以加引号，是因为我们想象空气是由一种分子质量为29.0的单一物质组成的，即质子质量的29倍)。

答:我们使用碰撞频率公式:~ noacvms = 2.69 × 1025个分子m-3 × 5 × 10-19 m2 × 485 ms-1 = 6.52 × 109个碰撞s-1。□

例2.6单位时间内，单位面积内与垂直于x轴的壁的典型碰撞次数是多少?设条件为STP。答:从左侧撞击壁面的分子数为(n0 / 4)(Av)，其中n0为分子数密度，A为壁面面积(1 m2)， v为2.3节中所示的分子平均速度。N0 = 2.69 x 1025分子m-3

v可以被看成是前面例子的VRMS。因此，在STP中，每秒大约有1027次与1平方米墙壁的碰撞。除数6从何而来?它来自于对所有角度的仔细整合，等等。一个简单的(但正确的)得到它的方法是注意到|个分子在x方向上，但只有一半的分子在+x方向上。不管有没有6，这是一个非常大的碰撞率。□

数学复习:概率密度函数(pdf)数量P (u) du是在(u, u + du)范围内找到变量u的概率。发现它有任何实际价值的概率是统一的;因此

u的均值定义为

它的方差或均方值由

变量u称为随机变量。在处理随机变量时，我们考虑变量的独立实现(就像从帽子中画值一样)。

继续阅读:可逆和不可逆功

这篇文章有用吗?

0 0