标量和向量场

一个标量场是一个函数定义在三维空间坐标和可能沿着时间轴。一个例子是温度场T (x, y, z;t) = t (r, t)的位置向量定义为r = x + y j + z k (9.17)

我和j, k是单位向量指向x, y和z轴(见图9.5)。小增量r表示为1

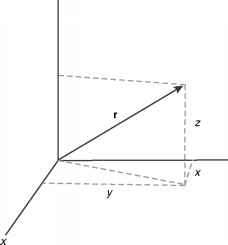
图9.5原理图的位置向量r的组件是x, y, z。

1我们取代小值Ax, Sx,等等,无穷小dx,等等,近似等号= ^取代的迹象。这意味着在这个符号二阶量(dx) 2等被忽视(设置为0)当添加剂一阶条件。虽然这个操作快捷方式可能会导致有些畏缩,它不应该打扰我们的故事。

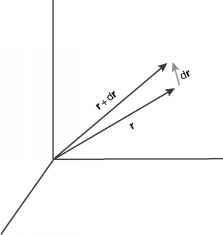
图9.6原理图的位置向量r博士和一个增量。

考虑温度场的估计在r +博士(图9.6),因为我们知道它的价值在r,即T (r):

我们可以用泰勒展开式的前两个条件:

d T d T dT (x + dx, y + dy, z + dz) = T (x, y, z) + - dx + - dy + dz。(9.19)

dx, dy dz

我们也可以把它写成一个点产品:

T (r +博士)= (r) +博士■VT (r)。后用dT = T (r +博士)- T (r),我们获得博士dT =■VT(标量场的微分)。

向量VT (r)称为梯度经常。我们将使用现代符号VT表示梯度(在一些老的文本表示毕业生T)。

(标量场的梯度)。

梯度是一个向量场。在每个空间r点都有一个关联的长度和方向。

如果你想知道的变化率在一个特定的方向,沿着方向定义的单位向量表示,n,它可以发现defining2向量增量博士nds, ds是无穷小的距离和n定义的方向沿着增量。使用(9.21)我们可以写博士

[n]方向导数。(9.23)

这导数沿指定方向的单位向量n称为方向导数,并且经常考虑到符号dt / dn的变化率T沿一定方向,定义的单位向量n。传统的方向导数的符号:

方向导数。(9.24)

如果n是切平面一个等温(仍然思维标量场的温度)表面,方向导数消失由于没有任何方向躺在这个平面上的变化。这意味着该组件(投影)的梯度向量的切线等温表面消失。梯度向量垂直于等温表面表面(一般所谓的水平)。这可以看出一个固定的梯度向量VT。只是不同各个方向的单位向量。n和VT的长度是固定的,所以最大值发生在n和v之间的夹角为零(因为0 n, VT = 1),换句话说当n平行于VT。

示例9.7考虑

T (x, y) = T0 cos 2 n x因为n y。(9.25)

找到梯度作为x和y的函数。

答:

VT (x, y) = - nT0 (2 sin2nx因为梭+ cos2nx罪nyj)。(9.26)的等值线图如图9.7所示。□

示例9.8发现场的方向导数在最后一个示例的方向n = (1 / V2) (i + j)(这是一个单位向量在x - y平面定向45°以上x轴)。

答:取点积的n梯度:

- n n•VT =(2罪2 nx因为纽约+ cos 2 nx罪纽约)。□

记住,读者有权选择博士,其微小的长度和方向。

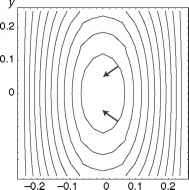
图9.7场的等值线图T (r) = cos2nx cos纽约显示常数T线。箭头指示方向的梯度向量评估点箭头起源的地方。

图9.7场的等值线图T (r) = cos2nx cos纽约显示常数T线。箭头指示方向的梯度向量评估点箭头起源的地方。

图9.8一个小长方体的边宽度dx, dy, dz,表明压力两边垂直于轴。

继续阅读:单位和数值常量

这篇文章有用吗?

0 1