热力学方程

在本章中，我们推导出大气科学的两个基本方程，连续性方程和热力学方程。连续性方程以偏微分方程的形式表示质量守恒，这种形式需要在数值模拟或预测中实现。热力学方程将热力学第一定律和第二定律组合成类似的形式。但是在我们讲这些重要的公式之前我们需要一些经验标量场和向量场．本章的大部分内容涉及基本向量分析，这些内容本应在微积分的前提课程中涵盖。因此，一些学生可以跳过复习部分，但我们建议所有学生都要复习。所有这些机器都是为了准备大气科学教育的下一步:动力学。

三维矢量，用黑体字A表示，是一个数学对象，它既有长度又有方向。在二维空间中，它可以用箭头表示，如图9.1所示。它需要三个数字来表示一个3向量，两个角和一个长度，(0,0;| |)。或者，它可以表示为沿着三个笛卡尔坐标轴(ax, ay, az)的三个分量。请注意，向量是空间中的一个抽象对象，与坐标系统的选择无关，但是指定它所需的三个数字可能单独依赖于分析人员用来描述向量所选择的坐标系统。例如，在气象学中，通常建立一个以地球表面某一点为原点的笛卡尔坐标系，x轴向东递增，y轴向北递增。

假设a是一个标量，即一个与我们选择的坐标系无关的数字，a是一个向量。一个向量乘以一个标量就可以写成b = aa。b方向与a方向相同，长度为|a||a|。换句话说，这两个角表示了b和a的方向

图9.1二维矢量a。

图9.1二维矢量a。

一样，但是长度拉长了。如果a是负的，向量的方向反过来。在笛卡尔分量表示的情况下，所有三个分量都乘以a:(aax, aay, aaz)。

两个向量的和是向量c = a + b，其分量由加数的笛卡尔分量相加定义:

(Cx, Cy, Cz) = (ax + bx, ay + by, az + bz)。(9.1)

显然，a + b = b + a。两个向量的和也可以从几何上理解为将一个向量的尾部与另一个向量的头部相连，连接第一个尾部与第二个头部的直线就是向量和。

笛卡尔单位向量单位向量是具有单位长度的向量。使用沿着三个笛卡尔轴的单位向量是非常方便和常见的:

这个符号允许我们将一个向量展开为它的笛卡尔分量a = axi + ayj + azk，或者(ax, ay, az)。(9.5)

a的长度由

|a| = yO?+ a2 + az2。注意矢量的长度与所选择的坐标系无关。

气象学中的风通常用v = ui + vj + wk表示。因此，风往东吹就是乌;如果u > 0，它被称为西风带。向北吹的风是vj;如果v > 0则称为偏南。上升气流(垂直风)记为wk。请注意，这些分量是指一个笛卡尔坐标系，其原点是在地球表面的一个固定位置。风速由Vu2 + v2 + w2给出。

求向量a = 2i + 3j - 4k的长度。

答案:|a| = V22 + 32 + (-4)2 = V29。□

求向量a = 2i + 3j - 4k, b = -4i + 3j + 2k的和。答案:a + b = -2i + 6j - 2k。□

有时使用曲线坐标系(如柱坐标系)来描述大气中的现象是有用的。我们使用单位向量指向圆柱坐标方向(取决于点):r, n, e, k。向量a可以写成:

A = ar + ae + az k. (9.7)

例9.3纯气旋风围绕一个活动中心逆时针(北半球)吹。在距离中心r处，风可记为ve(r, 0)n e.□

例9.4轴在圆盘中心的旋转圆盘上的一点的速度为ra>ne，其中m为在rad s-1内的角速度，r为旋转轴。□

向量更新:点积两个向量的点积或标量积得到一个标量。尽管构成标量积的两个向量的分量取决于坐标系的选择，但标量积却不是:

其中ea,b为两个向量之间的夹角，如图9.2所示。注意，由于cos ea,b是其参数的偶函数，乘积中向量的顺序没有区别:a■b = b■a。

另一种定义点积a■b的方法是a■b = axbx + ayby + azbz。(9.9)

可以证明这两个定义是等价的。使用第二个定义，

可以证明这两个定义是等价的。使用第二个定义，

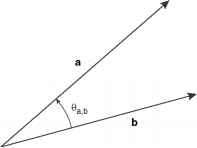
图9.2向量a和b在点积中的图示。

我们可以证明c■(a + b) = c■a + c■b。还清楚地知道i■i = 1, i■j = 0，等等。

例9.5求a■b，其中a = 2i + 3j - 4k, b = - 4i + 3j + 2k。

答:■b = (2) (4) + 3 x 3 + (4) x(2) = 7。□

例9.6 a与b的夹角是多少?

答案:cos6 = a■b/|a||b| = -7/29;Arccos(-7/29) = 1.815。□

向量或叉乘用c = a x b表示。

向量c垂直于a和b定义的平面(见图9.3)。右手定则用于确定其方向(将右手食指指向乘积中的第一个向量，然后将其扫向第二个向量的方向;拇指指向向量乘积的方向)。它的长度是

根据右手定则，我们看到:

a x b = - b x a。(9.12)a x b外积的一个有用的形式是

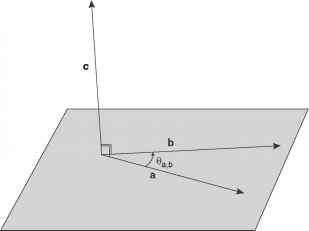
图9.3矢量c = a x b在叉乘中的图示。C垂直于a和b组成的平面。

	我	j	k
ax = b	斧头	唉	阿兹
	bx	通过	数学复习:3 x 3行列式回想一下，它可以沿着任何行或列展开。在叉乘的表示中: = i(aybz - azby) - j(axbz - azbx) + k(axby - aybx)。 回想一下单位向量的交替符号当一个向量沿着上面一行展开时。注意，如果行列式的两行(向量)成比例，行列式就会消失。这就是sin(0a,b) = 0。 我 j k 斧头 唉 阿兹 bx 通过 热晕 向量刷新器:盒子乘积。定义如下: a■(b x c) = c■(a x b) = b■(c x a)。盒子积的一个有用形式是 残雪 cy cz C■(a x b) = 斧头 唉 阿兹 ．(9.15) bx 通过 热晕 这三个向量a b c构成了一个平行六面体。盒积就是那个几何图形的体积。行列式的规则在这里很有用。例如，行的循环排列可以得到等价的行列式。互换相邻行会翻转符号。知道这三个向量是有用的 图9.4由向量a、b、c组成的平行六面体示意图。盒积a■b x c的大小就是平行六面体的体积。 图9.4由向量a、b、c组成的平行六面体示意图。盒积a■b x c的大小就是平行六面体的体积。 一个盒子的乘积可以被识别为一个立体平行六面体的三条边。盒积就是平行六面体的体积(见图9.4)。注意k (i x j) = 1。(9.16)

继续阅读:常数的单位和数值

这篇文章有用吗?

0 0