与吸收和散射光互动媒体
吸收系数(a),散射系数(a),和散射相functionp (a, 0),可以表示为:
我p (2,0) =) (9.4)
下标我是用来表示各种radiatively-active组件,即。,空气分子、气溶胶和液态水冰云粒子在大气中;在雪中冰晶和杂质;冰盐水口袋和气泡;纯净水与气泡混合,叶绿素、无机粒子,和黄色物质在海洋里。这里是波长,©散射角,这是有关极地和方位角度通过球面几何学的余弦定律:
因为0 = cos 0因为0 ' +罪罪0 ' cos (^ - < / > ')
之前在这里表示辐射方向散射,散射后的辐射方向。
9.2.4.1吸收和散射的大气分子和纯水
地球大气层吸收的分子是由于radiatively-active痕量气体。对紫外线和可见光最重要的臭氧气体,但的硫氧化物和氮氧化物(取决于位置)有显著影响紫外线辐射渗透。在相对原始的极地地区,我们可以假设紫外线和可见光,臭氧是唯一重要的吸收气体在大气中。因此,分子吸收系数就变成:
下标m代表分子,an0和臭氧是n0 ^吸收截面分别和数量密度(无花果。9.2 (a)、(b))。在波长超过310海里,臭氧吸收是由于哈金斯乐队,而spectrally-broad但弱吸收450和700 nm之间由于Chappuis乐队(图9.2 (a))。
分子散射的大气气体密度成正比。因此,由于空气分子散射的散射系数:
crn射线(A) ~ ~ 4是瑞利散射横截面,纳米是总空气数密度(图9.2 (b))。
吸收了纯水的结果相互之间的相互作用的分子间作用力。从第一原理计算吸收横截面是非常困难的。因此,实验室和现场测量(Pegau et al ., 1995;教皇和弗莱,1997)成为建立吸收系数的基本出全新(A)为纯水(图9.2 (c))。
波长(nm)波长(nm)
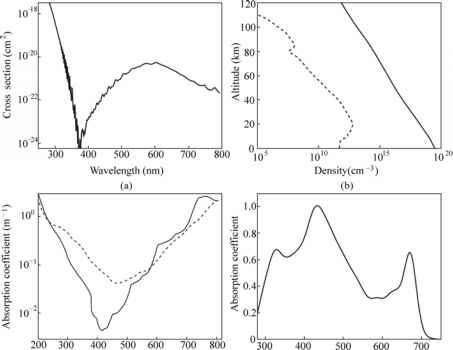
图9.2 (a)臭氧吸收截面;(b)数密度的大气臭氧总量(虚线)和空气数密度(实线);(c)吸收光谱纯冰(虚线)和纯水(实线;(d) chlorophyll-specific吸收光谱归一化在440海里
波长(nm)波长(nm)
图9.2 (a)臭氧吸收截面;(b)数密度的大气臭氧总量(虚线)和空气数密度(实线);(c)吸收光谱纯冰(虚线)和纯水(实线;(d) chlorophyll-specific吸收光谱归一化在440海里
纯水散射是由于集群的分子和离子,比光的波长小得多,从光学的角度来看,集群是不相关的(托马斯和Stamnes, 1999)。因此,对波长的依赖关系纯水的散射截面是crnw (A) ~ ~ 432,类似于大气中分子的瑞利散射截面。纯水的散射系数可近似(龙葵,1974):
被大气分子散射相位函数或纯水是由:
Pw (®) = 77 ^ -•(1 + x cos2 0) (3 + x)
供空气分子散射(瑞利散射),设置参数x等于1,而散射的纯净水,x = 0.835。后者x的值可以归因于水分子的各向异性(莫布里,1994;莫雷尔Gentili, 1991)。
9.2.4.2吸收和散射粒子
除了分子,悬浮颗粒物在大气和海洋辐射传递产生重大影响。颗粒物包括气溶胶(灰尘,硫酸盐颗粒,烟尘,烟雾粒子,云水滴,雨滴、冰晶,等等)在大气中,雪谷物、气泡和冰盐水里,花水(悬浮粒子有机和无机的起源)在水里。因此,为了描述辐射传输介质等耦合atmosphere-snow-ice-ocean(卡西欧)系统,我们可以认为它是由随机分布、radiatively-active“粒子”,吸收和散射辐射。
我们假设粒子的光学性质(即。雪、气溶胶、云粒子,谷物、盐水袋等)可以近似球体。吸收和散射系数和散射相函数可以写成:
(2)= J r % 2 qa (r) n博士(r) (9.7)
(2)J = ^ nr 2 qa (r) n博士(r) (9.8)
J n (r)博士在Qa (r)或Qa (r)被定义为吸收或散射截面的比值为一个半径为r的球形颗粒的几何截面nr2, n (r)粒度分布,r是每个粒子的半径。r的特定值,我们可以计算Qa (r)、Qa (r)和pp (2 0 r)使用Lorenz-Mie理论,但评估方程式。(9.7)- (9.9)r =需要知识
粒度分布n (r),这通常是未知的。
哈姆雷et al。(2004)表明,方程式。(9.7)-(9.9)可以大大简化做出以下假设:
•的粒度分布特点是一个有效半径
| m n (r) r 3 drj j“°“n (r) r 2博士,也不再需要一个集成/ r。
•粒子的弱吸收,所以
Qa (r) - - - - - - [mrel - (1) mrel”3 ' 2], p mi是虚部
的折射率的粒子,是真空的波长,mrel =先生/地中海先生的比例是粒子的折射率的实部(p)先生的周围介质(地中海先生)。
•粒子的波长相比很大(2 nr /»1),这意味着Qa (r) = 2。
•散射相函数可以表示为一个参数Henyey-Greenstein相位函数,它只取决于不对称
1 f1
美联社(A) =(一)■-•f (1 - (mr2d 1) 3/2) (9.10)
页(*”0)= (1 ^ 2 ^)3/2 (9.12)
在(a)的吸收系数是物质的粒子是什么
组成,阵线= - nr东北,东北是单位体积颗粒的数量和半径r。
9.2.4.3光学性质的海洋
代表冰下的水的光学特性,我们可以使用这个模型的龙葵(1991),更新龙葵和Maritorena(2001),根据吸收和散射系数和散射相函数给出了:
(一)= aw (a) + aC (a) + aY (a) (9.13)
^ 0)= w w ^ wQ) + w ^ ^ CQ) (9.15)
下标w表示纯水,下标C表示并且相关的吸收和散射,和下标Y代表黄色物质。上面讨论纯水的吸收系数(见图9.2 (c)),和ac (A) = 0.064 ac (A) C065
AC (A)的归一化吸收光谱吸收相关的并且显示在图9.2 (d)和C (mg•m ~ 3)是叶绿素A浓度。黄色物质的吸收表示为:
叹(A) =哎(440)实验[-0.014 (2 - 440)]
aY (440) = 0.2 (aw ac (440) (440) + 0.064 C065],并且相关的散射系数是由:
^ 550年
9.2.4.1散射在纯水中讨论部分。9.2.4.4辐照度的定义和光辉
光谱辐照度净阵线被定义为净能量d3E穿越表面元素dA(单位法n)单位时间和单位频率(托马斯和Stamnes, 1999):
F =——[W•m ~ 2•赫兹”。
由于辐照度是正的,如果能量流进半球集中在n和消极的方向如果流到相反的半球,我们可以定义光谱半球形辐照度F * = d3E + / dAdtdv和F ~ = d3E ~ / dAdtdv。因此,光谱辐照度净成为阵线= ^ - F ~
考虑任何小子集的能量d4 E立体角内流动dm在害怕方向2 dt的时间间隔和频率范围内的dv。如果这个子集的辐射经过表面元素dA(单位法n),然后单位立体角,单位面积上的能量频率,单位和单位时间内,定义了光谱辐射四:
4 = - - - - - - [W•m2■sr_1•赫兹1]。
cosOdAdtdmdv
这里d n曲面法线之间的角度和方向的传播。很明显从这些定义F * = J因为9第四
F ~ = 1 docos # 4。因此,光谱辐照度净可以表示为:
最后,我们平均强度定义为:I = (1/4 n) J d第四®,它只是平均光辉的球体。
9.2.4.5吸收、散射和灭绝的分子和粒子
一束光入射在薄层厚度ds radiatively-active物质(气体和/或颗粒)减毒的微分光辉成正比入射光:dIv = - k (v, s)试管,k (v, s)称为灭绝或衰减系数。集成的收益率
Iv(年代,12)= 4 (0,12)exp (ts (v)], (9.16)
12表示光束的传播方向。无因次灭绝(或衰减)光学路径(或不透明度)沿着路径是由f >年代rs (v) = J k (v,年代ds”)。衰减引起的光束可以吸收或散射。灭绝(或衰减)的光路/分子吸收和散射粒子的混合物被定义为散射和吸收光学路径的总和,rs (v) = rsc (v) + ra (v), rsc (v) = ^ J ds我(v s ')
我和ra (v) = ^ J特(v,年代”)。和结束所有光学活性的物种(每个我用下标)和<霁(v, s)和(v, s) (m - 1)散射和吸收系数,和ki (v, s) = ^ - (v, s) + ^ - (v, s)灭绝或衰减系数。这些被定义为cr; (v s) = ani (v)新泽西(s)和^ - (v, s) =
一个,我(V)倪(s),倪(m3)浓度和ani (V)和crni (V) (m2)的吸收和散射截面是第i个光学活性的物种(分子或粒子)。
9.2.5辐射传输方程
如果我们感兴趣的主要是在能量转移,而非定向辐射的依赖,它是足以与azimuthally-averaged光辉Iv (z, u),在z表示水平介质(大气中高度或深度海洋中),和u = cos ^, d极角。方便把辐射场分割成两个部分:(1)直接阳光,这是指数衰减在通过大气和海洋,和(2)扩散或散射辐射。
根据情商。(9.16),直接太阳光束穿过大气层的渗透可能写成隔离(年代,f2) = f s (£2 - Qf) e ~ Ts (v)。f20 =(#„、美元)是一个单位矢量的方向入射太阳光束,ju0 = cos # 0, 0 o是太阳天顶角见图9.3。Fs是太阳辐照度(正常害怕太阳射束方向2 0)事件的顶部的气氛。在平行平面几何,垂直光学深度定义的光路rs (v)如下:
我或博士(v, z) = - k (v, z) dz =;(z) +一个,我(z)]倪博士(z) dz (v, z) = - k (v, z) dz =;(z) +一个,我(z)]倪dz (z)
海洋
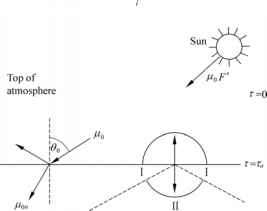
图9.3示意图说明两个相邻媒体与平面界面,如一个平静的海洋上空的大气。因为折射率的实部(mr)的大气(matm r»1)是不同的海洋(mocn r»1.33),大气中的辐射分布在老2 n将局限于锥小于2 n sr在海里(区域2)。海洋中的辐射区域内我将完全反映当从下面的接口(托马斯和Stamnes, 1999)
海洋
图9.3示意图说明两个相邻媒体与平面界面,如一个平静的海洋上空的大气。因为折射率的实部(mr)的大气(matm r»1)是不同的海洋(mocn r»1.33),大气中的辐射分布在老2 n将局限于锥小于2 n sr在海里(区域2)。海洋中的辐射区域内我将完全反映当从下面的接口(托马斯和Stamnes, 1999)
所以,平行平面介质直接组件变得:
/溶胶(r, u,美元)= FsS (u - ^(害怕——害怕K ^”(9.17)
这里u = cos0 d的极角观察方向,ju = \ u |, 0表示观察方向的方位角。
分层介质的光学特性变化只在垂直方向,并通过这样一个散射辐射的转移中所描述的:
u d / C ^ w) = _k (z) j (z, u) + ff (z)我f1 du p (z, u, u)我(z, u) + S \ z, u) (9.18) dz 2 j - 1
我(z, u)是azimuthally-averaged分散光辉。左边这个词在Eq。(9.18)是漫射辐射的变化我(z, u)沿着倾斜路径dz / u。右边第一项的损失的辐射光束由于灭绝,第二项是由于多次散射增益。第三项,S ' (z, u)下面的定义,是太阳能pseudo-source比例减毒太阳光束,它的驱动器的散射辐射。用无因次光学深度,博士(z) = - k d (z) z作为独立变量,我们可以重写Eq。(9.18)如下:
u d 1傻人)=我(T, u) _£(£) f1 du p (r u, u)我(r, u ') - S * (r, u) (9.19)
在单散射反照率被定义为(r (z)) = (z) / k (z)。
继续阅读:比较建模曹系统的辐照度
这篇文章有用吗?