理想生化反应器
几乎所有用于动力学研究的生物反应器,无论是间歇式反应器还是连续式反应器都是混合反应器的类型。下面几节将简要介绍两种混合良好的反应器:理想间歇反应器和理想连续流动搅拌槽反应堆(装运箱).
理想的间歇式反应器
在间歇反应器中,营养物质、底物、产物和细菌细胞的浓度随着微生物生长的进行而随时间变化。
摩尔物料平衡对间歇反应器中A组分的影响,得到如下关系式(式4.11):
D_ dt培养体积培养体积
^ f摩尔浓度^
组件A
摩尔:反应形成的物质
122食物和农业废水或,数学上可得(式4.12):
d (rR'CA > = VR rA
其中VR为培养体积,CA为摩尔浓度,rA为反应速率。批式反应器的容积不是培养容积VR,除非反应器已满。VR通常被认为是常数,只要没有从反应器中添加或移除液体。这一事实导致以下简化(式4.13):
为了计算组分A的浓度变化,需要对式4.13在t-t0(式4.14)的时间周期进行积分:
C直流
CA0是A时刻的浓度,t0。根据反应的阶数可以得到rA与t的关系函数;用第一章中描述的生化反应动力学方程可求解式4.14。
理想的plug-flow反应器
塞流式反应堆也称为活塞流式反应堆。所有离开栓流式反应器的材料都将在反应器中停留相同的时间。假设没有纵向混合或扩散。图4.3所示的塞流反应器的数学推导,可以基于组件A的反应器体积单元dV的物质平衡(式4.15):
输入-输出=反应消失,因为输入= FA,输出= FA + dFA
Fa = Fa + dFA + (_ rA)dV
-
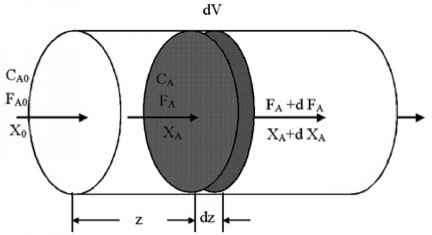
- 图4.3。一个plug-flow反应器的示意图。
其中FA为a物料的流速,因为d = d[FA0(1-XA)] = - FAodXA
所以公式4.15变成
这样可以综合生产控制方程对于plug-flow反应器,
C; d; C
T~T a ao
其中CA0 = FA0/V, rA可以是零、一级或二级反应。
-
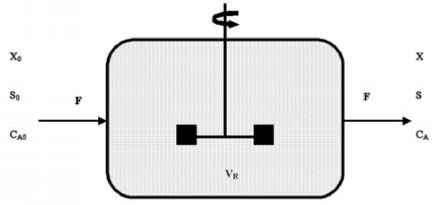
- 图4.4。CSTR型反应堆的示意图。
理想的连续搅拌釜式反应器(装运箱)
图4.4图示了CSTR型反应器。在cstr中,反应器内的液体是完全混合的。混合是通过一个叶轮或上升的气泡(通常是氧气),或两者兼有。CSTR最典型的特征是,它假定混合是彻底和完全的,因此任何相的浓度不随反应器内位置的变化而变化。
如图4.4所示,罐内溶解氧在整个散装液相中是相同的。由于反应器中氧气分布的均匀性,废水处理操作的CSTR具有只要氧气提供良好(不需要考虑讨厌的流体力学),就可以将曝气器或搅拌器与反应分离的优点,从而简化了工艺设计和优化。在稳态下,反应器内所有浓度与时间无关,可在反应器上应用以下物质平衡(式4.20):
加入反应器的速率
反应器内的累积速率
从反应器中去除的速率
将上式中的语句替换为数学符号可得(式4.21):
F(ca0 - ca) = - va
式中,F为进料液流和出水液流的体积流量。
将式4.21重新排列得到(式4.22):
rA = F (CA - CA0) = D(CA - CA0)
其中D = F/VR,称为稀释率。该术语描述了反应器在稳态条件下的保持时间或处理速率。它是通过的满箱容积的数量反应堆槽单位时间,等于反应器平均保持时间的倒数。
由于CSTR缺乏浓度的时间依赖性,因此反应器分析形式与间歇式反应器不同,CSTR具有定义明确,易于再现的反应器的优势,尽管成本相对较高,实现稳态需要较长时间,但CSTR经常用于许多细胞生长动力学研究。批式反应器,可以像一个密封的烧杯或烧瓶一样简单,并在培养箱振动器中同时大量使用,仍然因其廉价、快速和无限制的优点而广泛使用。无论使用何种类型的反应器,研究细胞生长动力学的目标应基于动力学的预期应用和使用范围。只有这样,实验的设计和实施才能制定出来。
继续阅读:完全混合充气泻湖CMAL
这篇文章有用吗?

