信息Kju

du / dt

-2rnv cos e

一个

Uv tan e a

1dp p0 dx

规模

U 2 / l

傻人

foW

威斯康辛大学/

U 2 /

美联社/波尔

环流

可达

纯

真空度

10 - 14

- 9

纯

墨西哥湾流

纯

10-4

真空度

10 - 13

10-7

10-4

对于大气和海洋中的大尺度运动，与因子1/a相关的球曲率项可以忽略不计，与垂直速度相关的科里奥利力项可以忽略不计。因此，水平动量方程可以简化为以下形式du

1dp +F—7- + fxp0 dx dv dt

P-plane近似

动力海洋学研究的许多实际问题都与比地球半径小得多的经向尺度有关。对于这类问题，球面几何可以近似地表示为一组水平曲面与局部球面切向的局部笛卡尔坐标。在这个新的坐标系中，科里奥利参数在局部笛卡尔坐标原点f = 2rn sin e ~ 2rn sin e0 + 2rn cos e0 (y - y0) / ax附近的泰勒展开近似

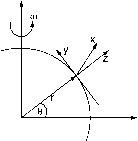
图2.22球坐标和局部定义的p平面示意图。

或f = fo + P (y - yo)， for \y - yo\^a (2.132)

其中P = 2m cos0o /a是行星涡度．使用局部笛卡尔坐标(图2.22)，我们有f = fo + py (2.132')

因此，在P平面近似下，相应的动量方程简化为du 1dp f v =—JL + Fx (2.133)

Dt Po y

注意，科里奥利参数是y的线性函数;因此，f的子午梯度等于p。p平面的引入大大降低了球几何和相关动力学的复杂性，使许多简单的分析研究可行。另一方面，p平面是一个近似，在Eqn约束下是有效的。(2.132);因此，对于水平尺度不满足Eqn的问题。(2.132)时，可以使用球坐标下的原方程。

对于更小尺度的运动，科里奥利参数的变化可以完全忽略;式(2.133)和(2.134)进一步简化为du 1 p fov =——f+ Fx (2.135)

Dt Po xdv 1p

Dt Po y

表2.8。三组坐标的比较

球面坐标j -平面f2«sin0

介绍j-平面和f -平面提供了非常简单和有用的工具大气学:对大气的研究还有海洋，而不涉及复杂的球面几何代数。然而，重要的是要记住，问题的一些基本要素在这些坐标中以略微不同的形式出现(见表2.8)。使用局部笛卡尔坐标可以简化方程，但也可能对动态图像产生微小的畸变。

2.6.4地质体与热风关系

对于盆地尺度的环流，与时间有关的项通常比科里奥利力项小得多，可以这样论证。让我们介绍罗斯比数，它被定义为与时间相关的项和科里奥利力项的比值

继续阅读:P0 d y

这篇文章有用吗?

0 0